
Hopf theorem
Encyclopedia
The Hopf theorem is a statement in differential topology
, saying that the topological degree
is the only homotopy invariant of continuous maps to spheres.
oriented manifold and Sn the n-sphere and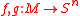 be continuous. Then
be continuous. Then 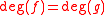 if and only if f and g are homotopic.
if and only if f and g are homotopic.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, saying that the topological degree
Degree of a continuous mapping
In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...
is the only homotopy invariant of continuous maps to spheres.
Formal statement
Let M be an n-dimensional compactClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
oriented manifold and Sn the n-sphere and
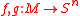 be continuous. Then
be continuous. Then 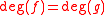 if and only if f and g are homotopic.
if and only if f and g are homotopic.

