Theory (mathematical logic)
Encyclopedia
In mathematical logic
, a theory (also called a formal theory) is a set of sentence
s in a formal language
. Usually a deductive system
is understood from context. An element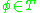
of a theory 
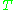is then called an axiom
of the theory, and any sentence that follows from the axioms (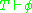
) is called a theorem
of the theory. Every axiom is also a theorem. A first-order theory is a set of first-order
sentences.
The construction of a theory begins by specifying a definite non-empty conceptual class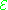
, the elements of which are called statements. These initial statements are often called the primitive elements or elementary statements of the theory, to distinguish them from other statements which may be derived from them.
A theory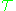
is a conceptual class consisting of certain of these elementary statements. The elementary statements which belong to 
are called the elementary theorems of 
and said to be true. In this way, a theory is a way of designating a subset of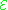 
which consists entirely of true statements.
This general way of designating a theory stipulates that the truth of any of its elementary statements is not known without reference to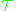
. Thus the same elementary statement may be true with respect to one theory, and not true with respect to another. This is as in ordinary language, where statements such as "He is a terrible person." cannot be judged to be true or false without reference to some interpretation of who "He" is and for that matter what a "terrible person" is under this theory.
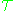is an inductive class. That is, that its content is based on some formal deductive system
and that some of its elementary statements are taken as axioms. In a deductive theory, any sentence which is a logical consequence of one or more of the axioms is also a sentence of that theory.
which is usually clear from context). In a deductive system (such as first-order logic) that satisfies the principle of explosion
, this is equivalent to requiring that there is no sentence φ such that both φ and its negation can be proved from the theory.
A satisfiable theory is a theory that has a model. This means there is a structure M that satisfies every sentence in the theory. Any satisfiable theory is syntactically consistent, because the structure satisfying the theory will satisfy exactly one of φ and the negation of φ, for each sentence φ.
A consistent theory is sometimes defined to be a syntactically consistent theory, and sometimes defined to be a satisfiable theory. For first-order logic
, the most important case, it follows from the completeness theorem
that the two meanings coincide. In other logics, such as second-order logic
, there are syntactically consistent theories that are not satisfiable, such as ω-inconsistent theories.
A complete consistent theory
(or just a complete theory) is a consistent theory T such that for every sentence φ in its language, either φ is provable from T or T
{φ} is inconsistent. For theories closed under logical consequence, this means that for every sentence φ, either φ or its negation is contained in the theory. An incomplete theory is a consistent theory that is not complete.
See also ω-consistent theory for a stronger notion of consistency.
has several associated theories. The complete theory of a structure A is the set of all first-order
sentence
s over the signature
of A which are satisfied by A. It is denoted by Th(A). More generally, the theory of K, a class of σ-structures, is the set of all first-order σ-sentences that are satisfied by all structures in K, and is denoted by Th(K). Clearly Th(A) = Th({A}). These notions can also be defined with respect to other logics.
For each σ-structure A, there are several associated theories in a larger signature σ' that extends σ by adding one new constant symbol for each element of the domain of A. (If the new constant symbols are identified with the elements of A which they represent, σ' can be taken to be σ
A.) The cardinality of σ' is thus the larger of the cardinality of σ and the cardinality of A.
The diagram of A consists of all atomic or negated atomic σ'-sentences that are satisfied by A and is denoted by diagA. The positive diagram of A is the set of all atomic σ'-sentences which A satisfies. It is denoted by diag+A. The elementary diagram of A is the set eldiagA of all first-order σ'-sentences that are satisfied by A or, equivalently, the complete (first-order) theory of the natural expansion of A to the signature σ'.
is a set of sentences in a first-order formal language
.
A is a syntactic consequence of a first-order theory
if there is a derivation
of A using only formulas in
as non-logical axioms. Such a formula A is also called a theorem of 
. The notation "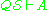
" indicates A is a theorem of 
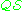is an interpretation in which every formula of 
is satisfied.
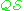is a first-order theory with identity if 
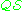includes the identity relation symbol "=" and the reflexivity and substitution axiom schemes for this symbol.
s in a particular language. The theory can be taken to include just those axioms, or their logical or provable consequences, as desired. Theories obtained this way include ZFC and Peano arithmetic.
A second way to specify a theory is to begin with a structure
and then let the theory be the set of formulas that are satisfied by the structure. This is one method for producing complete theories, described below. Examples of theories of this sort include the sets of true sentences in the structures (N, +, ×, 0, 1, =) and (R, +, ×, 0, 1, =), where N is the set of natural numbers and R is the set of real numbers. The first of these, called the theory of true arithmetic
, cannot be written as the set of logical consequences of any enumerable set of axioms.
The theory of (R, +, ×, 0, 1, =) was shown by Tarski to be decidable
; it is the theory of real closed fields.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a theory (also called a formal theory) is a set of sentence
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
s in a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. Usually a deductive system
Deductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
is understood from context. An element
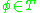of a theory 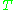is then called an axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of the theory, and any sentence that follows from the axioms (
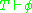) is called a theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of the theory. Every axiom is also a theorem. A first-order theory is a set of first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
sentences.
Theories expressed in formal language generally
When defining theories for foundational purposes, additional care must be taken and normal set-theoretic language may not be appropriate.The construction of a theory begins by specifying a definite non-empty conceptual class
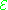, the elements of which are called statements. These initial statements are often called the primitive elements or elementary statements of the theory, to distinguish them from other statements which may be derived from them.A theory
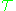is a conceptual class consisting of certain of these elementary statements. The elementary statements which belong to are called the elementary theorems of and said to be true. In this way, a theory is a way of designating a subset of 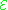which consists entirely of true statements.This general way of designating a theory stipulates that the truth of any of its elementary statements is not known without reference to
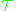. Thus the same elementary statement may be true with respect to one theory, and not true with respect to another. This is as in ordinary language, where statements such as "He is a terrible person." cannot be judged to be true or false without reference to some interpretation of who "He" is and for that matter what a "terrible person" is under this theory. Subtheories and extensions
A theory S is a subtheory of a theory T if S is a subset of T. If T is a subset of S then S is an extension or supertheory of TDeductive theories
A theory is said to be a deductive theory if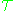 is an inductive class. That is, that its content is based on some formal deductive systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
and that some of its elementary statements are taken as axioms. In a deductive theory, any sentence which is a logical consequence of one or more of the axioms is also a sentence of that theory.
Consistency and completeness
A syntactically consistent theory is a theory from which not every sentence in the underlying language can be proved (with respect to some deductive systemDeductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
which is usually clear from context). In a deductive system (such as first-order logic) that satisfies the principle of explosion
Principle of explosion
The principle of explosion, or the principle of Pseudo-Scotus, is the law of classical logic and intuitionistic and similar systems of logic, according to which any statement can be proven from a contradiction...
, this is equivalent to requiring that there is no sentence φ such that both φ and its negation can be proved from the theory.
A satisfiable theory is a theory that has a model. This means there is a structure M that satisfies every sentence in the theory. Any satisfiable theory is syntactically consistent, because the structure satisfying the theory will satisfy exactly one of φ and the negation of φ, for each sentence φ.
A consistent theory is sometimes defined to be a syntactically consistent theory, and sometimes defined to be a satisfiable theory. For first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, the most important case, it follows from the completeness theorem
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
that the two meanings coincide. In other logics, such as second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
, there are syntactically consistent theories that are not satisfiable, such as ω-inconsistent theories.
A complete consistent theory
Complete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
(or just a complete theory) is a consistent theory T such that for every sentence φ in its language, either φ is provable from T or T
{φ} is inconsistent. For theories closed under logical consequence, this means that for every sentence φ, either φ or its negation is contained in the theory. An incomplete theory is a consistent theory that is not complete.See also ω-consistent theory for a stronger notion of consistency.
Interpretation of a theory
An interpretation of a theory is the relationship between a theory and some contensive subject matter when there is a many-to-one correspondence between certain elementary statements of the theory, and certain contensive statements related to the subject matter. If every elementary statement in the theory has a contensive correspondent it is called a full interpretation, otherwise it is called a partial interpretation.Theories associated with a structure
Each structureStructure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
has several associated theories. The complete theory of a structure A is the set of all first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
sentence
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
s over the signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
of A which are satisfied by A. It is denoted by Th(A). More generally, the theory of K, a class of σ-structures, is the set of all first-order σ-sentences that are satisfied by all structures in K, and is denoted by Th(K). Clearly Th(A) = Th({A}). These notions can also be defined with respect to other logics.
For each σ-structure A, there are several associated theories in a larger signature σ' that extends σ by adding one new constant symbol for each element of the domain of A. (If the new constant symbols are identified with the elements of A which they represent, σ' can be taken to be σ
A.) The cardinality of σ' is thus the larger of the cardinality of σ and the cardinality of A.The diagram of A consists of all atomic or negated atomic σ'-sentences that are satisfied by A and is denoted by diagA. The positive diagram of A is the set of all atomic σ'-sentences which A satisfies. It is denoted by diag+A. The elementary diagram of A is the set eldiagA of all first-order σ'-sentences that are satisfied by A or, equivalently, the complete (first-order) theory of the natural expansion of A to the signature σ'.
First-order theories
A first-order theory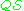 is a set of sentences in a first-order formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
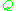.Derivation in a first order theory
There are many formal derivation ("proof") systems for first-order logic.Syntactic consequence in a first order theory
A formulaWell-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
A is a syntactic consequence of a first-order theory
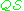if there is a derivationFormal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
of A using only formulas in
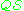as non-logical axioms. Such a formula A is also called a theorem of . The notation "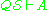" indicates A is a theorem of Interpretation of a first order theory
An interpretation of a first-order theory provides a semantics for the formulas of the theory. An interpretation is said to satisfy a formula if the formula is true according to the interpretation. A model of a first order theory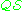 is an interpretation in which every formula of is satisfied.First order theories with identity
A first order theory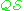 is a first-order theory with identity if 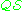includes the identity relation symbol "=" and the reflexivity and substitution axiom schemes for this symbol.Topics related to first order theories
- Compactness theoremCompactness theoremIn mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
- Consistent set
- Deduction theoremDeduction theoremIn mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
- Enumeration theorem
- Lindenbaum's lemmaLindenbaum's lemmaIn mathematical logic, Lindenbaum's lemma states that any consistent theory of predicate logic can be extended to a complete consistent theory. It is used in the proof of Gödel's completeness theorem, among other places...
- Lowenheim-Skolem theorem
Examples
One way to specify a theory is to define a set of axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s in a particular language. The theory can be taken to include just those axioms, or their logical or provable consequences, as desired. Theories obtained this way include ZFC and Peano arithmetic.
A second way to specify a theory is to begin with a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
and then let the theory be the set of formulas that are satisfied by the structure. This is one method for producing complete theories, described below. Examples of theories of this sort include the sets of true sentences in the structures (N, +, ×, 0, 1, =) and (R, +, ×, 0, 1, =), where N is the set of natural numbers and R is the set of real numbers. The first of these, called the theory of true arithmetic
True arithmetic
In mathematical logic, true arithmetic is the theory Th of the natural numbers in the language of first-order Peano arithmetic...
, cannot be written as the set of logical consequences of any enumerable set of axioms.
The theory of (R, +, ×, 0, 1, =) was shown by Tarski to be decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
; it is the theory of real closed fields.