
Arithmetical set
Encyclopedia
In mathematical logic
, an arithmetical set (or arithmetic set) is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic. The arithmetical sets are classified by the arithmetical hierarchy
.
A function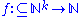 is called arithmetically definable if the graph
is called arithmetically definable if the graph
of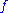 is an arithmetical set.
is an arithmetical set.
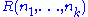 is arithmetical if there is a formula
is arithmetical if there is a formula
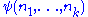 such that
such that  holds for all k-tuples
holds for all k-tuples  of natural numbers.
of natural numbers.
A finitary
function on the natural numbers is called arithmetical if its graph is an arithmetical binary relation.
A set A is said to be arithmetical in a set B if A is definable by an arithmetical formula which has B as a set parameter.
A set Y of natural numbers is implicitly arithmetical or implicitly arithmetically definable if it is definable with an arithmetical formula that is able to use Y as a parameter. That is, if there is a formula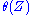 in the language of Peano arithmetic with no free number variables and a new set parameter Z and set membership relation
in the language of Peano arithmetic with no free number variables and a new set parameter Z and set membership relation  such that Y is the unique set such that
such that Y is the unique set such that 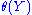 holds.
holds.
Every arithmetical set is implicitly arithmetical; if X is arithmetically defined by φ(n) then it is implicitly defined by the formula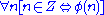 .
.
Not every implicitly arithmetical set is arithmetical, however. In particular, the truth set of first order arithmetic is implicitly arithmetical but not arithmetical.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, an arithmetical set (or arithmetic set) is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic. The arithmetical sets are classified by the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
.
A function
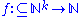 is called arithmetically definable if the graph
is called arithmetically definable if the graphGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of
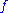 is an arithmetical set.
is an arithmetical set.Formal definition
A set X of natural numbers is arithmetical or arithmetically definable if there is a formula φ(n) in the language of Peano arithmetic such that each number n is in X if and only if φ(n) holds in the standard model of arithmetic. Similarly, a k-ary relation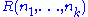 is arithmetical if there is a formula
is arithmetical if there is a formula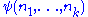 such that
such that  holds for all k-tuples
holds for all k-tuples  of natural numbers.
of natural numbers.A finitary
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
function on the natural numbers is called arithmetical if its graph is an arithmetical binary relation.
A set A is said to be arithmetical in a set B if A is definable by an arithmetical formula which has B as a set parameter.
Examples
- The set of all prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s is arithmetical. - Every recursively enumerable setRecursively enumerable setIn computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
is arithmetical. - Every computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
is arithmetically definable. - The set encoding the Halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
is arithmetical. - Chaitin's constantChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
Ω is encoded by an arithmetical set. - Tarski's indefinability theoremTarski's indefinability theoremTarski's undefinability theorem, stated and proved by Alfred Tarski in 1936, is an important limitative result in mathematical logic, the foundations of mathematics, and in formal semantics...
shows that the set of Gödel numbers of true formulas of first order arithmetic is not arithmetically definable.
Properties
- The complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of an arithmetical set is an arithmetical set. - The Turing jumpTuring jumpIn computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
of an arithmetical set is an arithmetical set. - The collection of arithmetical sets is countable, but there is no arithmetically definable sequence that enumerates all arithmetical sets.
Implicitly arithmetical sets
Each arithmetical set has an arithmetical formula which tells whether particular numbers are in the set. An alternative notion of definability allows for a formula that does not tell whether particular numbers are in the set but tells whether the set itself satisfies some arithmetical property.A set Y of natural numbers is implicitly arithmetical or implicitly arithmetically definable if it is definable with an arithmetical formula that is able to use Y as a parameter. That is, if there is a formula
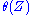 in the language of Peano arithmetic with no free number variables and a new set parameter Z and set membership relation
in the language of Peano arithmetic with no free number variables and a new set parameter Z and set membership relation  such that Y is the unique set such that
such that Y is the unique set such that 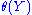 holds.
holds.Every arithmetical set is implicitly arithmetical; if X is arithmetically defined by φ(n) then it is implicitly defined by the formula
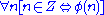 .
.Not every implicitly arithmetical set is arithmetical, however. In particular, the truth set of first order arithmetic is implicitly arithmetical but not arithmetical.

