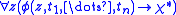Extension by definitions
Encyclopedia
In mathematical logic
, more specifically in the proof theory
of first-order theories
, extensions by definitions formalize the introduction of new symbols by means of a definition. For example, it is common in naive set theory
to introduce a symbol for the set which has no member. In the formal setting of first-order theories, this can be done by adding to the theory a new constant
for the set which has no member. In the formal setting of first-order theories, this can be done by adding to the theory a new constant  and the new axiom
and the new axiom
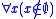 , meaning 'for all x, x is not a member of
, meaning 'for all x, x is not a member of  '. It can then be proved that doing so adds essentially nothing to the old theory, as should be expected from a definition. More precisely, the new theory is a conservative extension
'. It can then be proved that doing so adds essentially nothing to the old theory, as should be expected from a definition. More precisely, the new theory is a conservative extension
of the old one.
 be a first-order theory and
be a first-order theory and 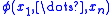 a formula of
a formula of  such that
such that 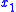 , ...,
, ..., 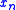 are distinct and include the variables free in
are distinct and include the variables free in 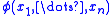 . Form a new first-order theory
. Form a new first-order theory  from
from  by adding a new
by adding a new  -ary relation symbol
-ary relation symbol  , the logical axioms featuring the symbol
, the logical axioms featuring the symbol  and the new axiom
and the new axiom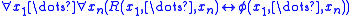 ,
,
called the defining axiom of .
.
If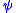 is a formula of
is a formula of 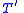 , let
, let  be the formula of
be the formula of  obtained from
obtained from 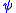 by replacing any occurrence of
by replacing any occurrence of 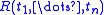 by
by 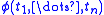 (changing the bound variables in
(changing the bound variables in  if necessary so that the variables occurring in the
if necessary so that the variables occurring in the 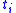 are not bound in
are not bound in 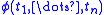 ). Then the following hold:
). Then the following hold:
The fact that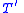 is a conservative extension of
is a conservative extension of  shows that the defining axiom of
shows that the defining axiom of  cannot be used to prove new theorems. The formula
cannot be used to prove new theorems. The formula  is called a translation of
is called a translation of 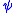 into
into  . Semantically, the formula
. Semantically, the formula  has the same meaning as
has the same meaning as  , but the defined symbol
, but the defined symbol  has been eliminated.
has been eliminated.
 be a first-order theory (with equality) and
be a first-order theory (with equality) and  a formula of
a formula of  such that
such that  ,
, 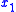 , ...,
, ..., 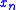 are distinct and include the variables free in
are distinct and include the variables free in 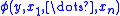 . Assume that we can prove
. Assume that we can prove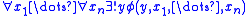
in , i.e. for all
, i.e. for all 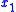 , ...,
, ..., 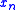 , there exists a unique y such that
, there exists a unique y such that 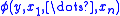 . Form a new first-order theory
. Form a new first-order theory 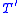 from
from  by adding a new
by adding a new  -ary function symbol
-ary function symbol 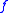 , the logical axioms featuring the symbol
, the logical axioms featuring the symbol 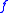 and the new axiom
and the new axiom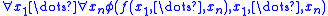 ,
,
called the defining axiom of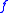 .
.
If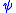 is an atomic formula
is an atomic formula
of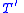 , define a formula
, define a formula  of
of  recursively as follows. If the new symbol
recursively as follows. If the new symbol 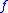 does not occur in
does not occur in 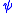 , let
, let  be
be 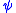 . Otherwise, choose an occurrence of
. Otherwise, choose an occurrence of 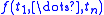 in
in 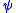 , and let
, and let  be obtained from
be obtained from 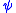 be replacing that occurrence by a new variable
be replacing that occurrence by a new variable  . Then since
. Then since 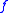 occurs in
occurs in  one less time than in
one less time than in 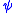 , the formula
, the formula  has already been defined, and we let
has already been defined, and we let  be
be
(changing the bound variables in if necessary so that the variables occurring in the
if necessary so that the variables occurring in the 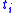 are not bound in
are not bound in 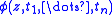 ). For a general formula
). For a general formula 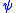 , the formula
, the formula  is formed by replacing every occurrence of an atomic subformula
is formed by replacing every occurrence of an atomic subformula  by
by 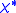 . Then the following hold:
. Then the following hold:
The formula is called a translation of
is called a translation of 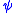 into
into  . As in the case of relation symbols, the formula
. As in the case of relation symbols, the formula  has the same meaning as
has the same meaning as 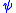 , but the new symbol
, but the new symbol 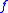 has been eliminated.
has been eliminated.
The construction of this paragraph also works for constants, which can be viewed as 0-ary function symbols.
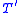 obtained from
obtained from  by successive introductions of relation symbols and function symbols as above is called an extension by definitions of
by successive introductions of relation symbols and function symbols as above is called an extension by definitions of  . Then
. Then 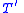 is a conservative extension of
is a conservative extension of  , and for any formula
, and for any formula 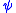 of
of 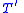 we can form a formula
we can form a formula  of
of  , called a translation of
, called a translation of 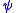 into
into  , such that
, such that 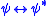 is provable in
is provable in 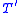 . Such a formula is not unique, but any two of them can be proved to be equivalent in T.
. Such a formula is not unique, but any two of them can be proved to be equivalent in T.
In practice, an extension by definitions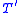 of T is not distinguished from the original theory T. In fact, the formulas of
of T is not distinguished from the original theory T. In fact, the formulas of 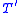 can be thought of as abbreviating their translations into T. The manipulation of these abbreviations as actual formulas is then justified by the fact that extensions by definitions are conservative.
can be thought of as abbreviating their translations into T. The manipulation of these abbreviations as actual formulas is then justified by the fact that extensions by definitions are conservative.
and what we obtain is an extension by definitions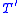 of T. Then in
of T. Then in 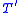 we can prove that for every x, there exists a unique y such that x.y=y.x=e. Consequently, the first-order theory
we can prove that for every x, there exists a unique y such that x.y=y.x=e. Consequently, the first-order theory  obtained from
obtained from 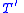 by adding a unary function symbol
by adding a unary function symbol 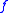 and the axiom
and the axiom
is an extension by definitions of T. Usually,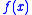 is denoted
is denoted 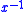 .
.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, more specifically in the proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
of first-order theories
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, extensions by definitions formalize the introduction of new symbols by means of a definition. For example, it is common in naive set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
to introduce a symbol
 for the set which has no member. In the formal setting of first-order theories, this can be done by adding to the theory a new constant
for the set which has no member. In the formal setting of first-order theories, this can be done by adding to the theory a new constant  and the new axiom
and the new axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
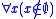 , meaning 'for all x, x is not a member of
, meaning 'for all x, x is not a member of  '. It can then be proved that doing so adds essentially nothing to the old theory, as should be expected from a definition. More precisely, the new theory is a conservative extension
'. It can then be proved that doing so adds essentially nothing to the old theory, as should be expected from a definition. More precisely, the new theory is a conservative extensionConservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of the old one.
Definition of relation symbols
Let be a first-order theory and
be a first-order theory and 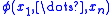 a formula of
a formula of  such that
such that 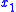 , ...,
, ..., 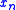 are distinct and include the variables free in
are distinct and include the variables free in 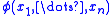 . Form a new first-order theory
. Form a new first-order theory  from
from  by adding a new
by adding a new  -ary relation symbol
-ary relation symbol  , the logical axioms featuring the symbol
, the logical axioms featuring the symbol  and the new axiom
and the new axiom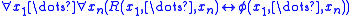 ,
,called the defining axiom of
 .
.If
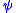 is a formula of
is a formula of 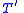 , let
, let  be the formula of
be the formula of  obtained from
obtained from 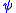 by replacing any occurrence of
by replacing any occurrence of 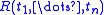 by
by 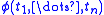 (changing the bound variables in
(changing the bound variables in  if necessary so that the variables occurring in the
if necessary so that the variables occurring in the 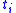 are not bound in
are not bound in 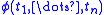 ). Then the following hold:
). Then the following hold:-
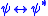 is provable in
is provable in 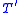 , and
, and -
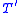 is a conservative extensionConservative extensionIn mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
is a conservative extensionConservative extensionIn mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of .
.
The fact that
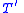 is a conservative extension of
is a conservative extension of  shows that the defining axiom of
shows that the defining axiom of  cannot be used to prove new theorems. The formula
cannot be used to prove new theorems. The formula  is called a translation of
is called a translation of 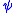 into
into  . Semantically, the formula
. Semantically, the formula  has the same meaning as
has the same meaning as  , but the defined symbol
, but the defined symbol  has been eliminated.
has been eliminated.Definition of function symbols
Let be a first-order theory (with equality) and
be a first-order theory (with equality) and  a formula of
a formula of  such that
such that  ,
, 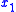 , ...,
, ..., 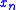 are distinct and include the variables free in
are distinct and include the variables free in 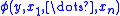 . Assume that we can prove
. Assume that we can prove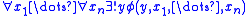
in
 , i.e. for all
, i.e. for all 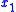 , ...,
, ..., 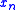 , there exists a unique y such that
, there exists a unique y such that 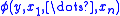 . Form a new first-order theory
. Form a new first-order theory 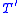 from
from  by adding a new
by adding a new  -ary function symbol
-ary function symbol 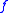 , the logical axioms featuring the symbol
, the logical axioms featuring the symbol 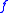 and the new axiom
and the new axiom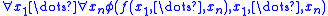 ,
,called the defining axiom of
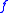 .
.If
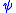 is an atomic formula
is an atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
of
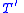 , define a formula
, define a formula  of
of  recursively as follows. If the new symbol
recursively as follows. If the new symbol 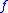 does not occur in
does not occur in 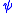 , let
, let  be
be 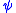 . Otherwise, choose an occurrence of
. Otherwise, choose an occurrence of 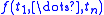 in
in 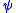 , and let
, and let  be obtained from
be obtained from 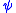 be replacing that occurrence by a new variable
be replacing that occurrence by a new variable  . Then since
. Then since 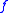 occurs in
occurs in  one less time than in
one less time than in 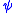 , the formula
, the formula  has already been defined, and we let
has already been defined, and we let  be
be
(changing the bound variables in
 if necessary so that the variables occurring in the
if necessary so that the variables occurring in the 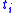 are not bound in
are not bound in 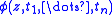 ). For a general formula
). For a general formula 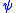 , the formula
, the formula  is formed by replacing every occurrence of an atomic subformula
is formed by replacing every occurrence of an atomic subformula  by
by 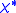 . Then the following hold:
. Then the following hold:-
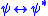 is provable in
is provable in 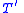 , and
, and -
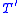 is a conservative extensionConservative extensionIn mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
is a conservative extensionConservative extensionIn mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of .
.
The formula
 is called a translation of
is called a translation of 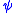 into
into  . As in the case of relation symbols, the formula
. As in the case of relation symbols, the formula  has the same meaning as
has the same meaning as 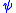 , but the new symbol
, but the new symbol 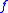 has been eliminated.
has been eliminated.The construction of this paragraph also works for constants, which can be viewed as 0-ary function symbols.
Extensions by definitions
A first-order theory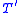 obtained from
obtained from  by successive introductions of relation symbols and function symbols as above is called an extension by definitions of
by successive introductions of relation symbols and function symbols as above is called an extension by definitions of  . Then
. Then 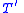 is a conservative extension of
is a conservative extension of  , and for any formula
, and for any formula 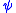 of
of 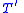 we can form a formula
we can form a formula  of
of  , called a translation of
, called a translation of 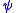 into
into  , such that
, such that 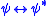 is provable in
is provable in 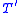 . Such a formula is not unique, but any two of them can be proved to be equivalent in T.
. Such a formula is not unique, but any two of them can be proved to be equivalent in T.In practice, an extension by definitions
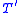 of T is not distinguished from the original theory T. In fact, the formulas of
of T is not distinguished from the original theory T. In fact, the formulas of 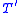 can be thought of as abbreviating their translations into T. The manipulation of these abbreviations as actual formulas is then justified by the fact that extensions by definitions are conservative.
can be thought of as abbreviating their translations into T. The manipulation of these abbreviations as actual formulas is then justified by the fact that extensions by definitions are conservative.Examples
- Traditionally, the first-order set theory ZF has
 (equality) and
(equality) and  (membership) as its only primitive relation symbols, and no function symbols. In everyday mathematics, however, many other symbols are used such as the binary relation symbol
(membership) as its only primitive relation symbols, and no function symbols. In everyday mathematics, however, many other symbols are used such as the binary relation symbol 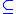 , the constant
, the constant  , the unary function symbol P (the power-set operation), etc. All of these symbols belong in fact to extensions by definitions of ZF.
, the unary function symbol P (the power-set operation), etc. All of these symbols belong in fact to extensions by definitions of ZF.
- Let
 be a first-order theory for groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
be a first-order theory for groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
in which the only primitive symbol is the binary product . In T, we can prove that there exists a unique element y such that x.y=y.x=x for every x. Therefore we can add to T a new constant e and the axiom
. In T, we can prove that there exists a unique element y such that x.y=y.x=x for every x. Therefore we can add to T a new constant e and the axiom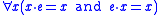 ,
,
and what we obtain is an extension by definitions
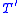 of T. Then in
of T. Then in 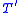 we can prove that for every x, there exists a unique y such that x.y=y.x=e. Consequently, the first-order theory
we can prove that for every x, there exists a unique y such that x.y=y.x=e. Consequently, the first-order theory  obtained from
obtained from 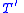 by adding a unary function symbol
by adding a unary function symbol 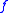 and the axiom
and the axiom
is an extension by definitions of T. Usually,
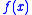 is denoted
is denoted 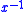 .
.