Critical phenomena
Encyclopedia
In physics
, critical phenomena is the collective name associated with the
physics of critical point
s. Most of them stem from the divergence of the
correlation length, but also the dynamics slows down. Critical phenomena include scaling
relations among different quantities, power-law divergences of some quantities (such as the magnetic susceptibility
in the ferromagnetic phase transition
) described by critical exponent
s, universality
, fractal
behaviour, ergodicity
breaking. Critical phenomena take place in second order phase transition, although not exclusively.
The critical behavior is usually different from the mean-field approximation
which is valid away from the phase transition, since the latter neglects correlations, which become increasingly important as the system approaches the critical point where the correlation length diverges. Many properties of the critical behavior of a system can be derived in the framework of the renormalization group
.
In order to explain the physical origin of these phenomena, we shall use the Ising model
as a pedagogical example.
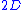square array of classical spins which may only take two positions: +1 and −1, at a certain temperature 
, interacting through the Ising
classical Hamiltonian
:
where the sum is extended over the pairs of nearest neighbours and
is a coupling constant, which we will consider to be fixed. There is a certain temperature, called the Curie temperature or critical temperature, 
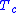below which the system presents ferromagnetic long range order. Above it, it is paramagnetic and is apparently disordered.
At temperature zero, the system may only take one global sign, either +1 or -1. At higher temperatures, but below
, the state is still globally magnetized, but clusters of the opposite sign appears. As the temperature increases, these clusters start to contain smaller clusters themselves, in a typical Russian dolls picture. Their typical size, called the correlation length, 
grows with temperature until it diverges at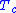 
. This means that the whole system is such a cluster, and there is no global magnetization. Above that temperature, the system is globally disordered, but with ordered clusters within it, whose size is again called correlation length, but it is now decreasing with temperature. At infinite temperature, it is again zero, with the system fully disordered.
, 
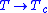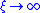. This divergence poses no physical problem. Other physical observables diverge at this point, leading to some confusion at the beginning.
The most important is susceptibility
. Let us apply a very small magnetic field to the
system in the critical point. A very small magnetic field is not able to magnetize a large coherent cluster, but with these fractal
clusters the picture changes. It affects easily the smallest size clusters, since they have a nearly paramagnetic behaviour. But this change, in its turn, affects the next-scale clusters, and the perturbation climbs the ladder until the whole system changes radically. Thus, critical systems are very sensitive to small changes in the environment.
Other observables, such as the specific heat, may also diverge at this point. All these divergences stem from that of the correlation length.
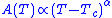for some exponent 
where, typically, the value of the exponent α is the same above and below Tc. These exponents are called critical exponents and are robust observables. Even more, they take the same values for very different physical systems. This intriguing phenomenon, called universality
, is explained, qualitatively and also quantitatively, by the renormalization group
.
of a system is directly related to the divergence of the thermal correlation length 
by the introduction of a dynamical exponent z and the relation 
. The voluminous static universality class of a system splits into different, less voluminous dynamic universality classes with different values of z
but a common static critical behaviour, and by approaching the critical point one may observe all kinds of slowing-down phenomena.
is the assumption that a system, at a given temperature, explores the full phase space, just each state takes different probabilities. In an Ising ferromagnet below
this does not happen. If 
, never mind how close they are, the system has chosen a global magnetization, and the phase space is divided into two regions. From one of them it is impossible to reach the other, unless a magnetic field is applied, or temperature is raised above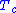 
.
See also superselection sector
, which takes advantage of the Russian dolls picture to explain universality and predict numerically the critical exponents, and Variational perturbation theory, which converts divergent perturbation expansions into convergent strong-coupling expansions relevant to critical phenomena. In two-dimensional systems, Conformal field theory
is a powerful tool which has discovered many new properties of 2D critical systems, employing the fact that scale invariance, along with a few other requisites, leads to an infinite symmetry group
.
. For example, it is natural to describe a system of two political parties by an Ising model. Thereby, at a transition between one majority to the other one the above-mentioned critical phenomena may appear.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, critical phenomena is the collective name associated with the
physics of critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
s. Most of them stem from the divergence of the
correlation length, but also the dynamics slows down. Critical phenomena include scaling
Scaling
Scaling may refer to:* Scaling , a linear transformation that enlarges or diminishes objects* Reduced scales of semiconductor device fabrication processes...
relations among different quantities, power-law divergences of some quantities (such as the magnetic susceptibility
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
in the ferromagnetic phase transition
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
) described by critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s, universality
Universality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
, fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
behaviour, ergodicity
Ergodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
breaking. Critical phenomena take place in second order phase transition, although not exclusively.
The critical behavior is usually different from the mean-field approximation
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
which is valid away from the phase transition, since the latter neglects correlations, which become increasingly important as the system approaches the critical point where the correlation length diverges. Many properties of the critical behavior of a system can be derived in the framework of the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.
In order to explain the physical origin of these phenomena, we shall use the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
as a pedagogical example.
The critical point of the 2D Ising model
Let us consider a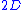 square array of classical spins which may only take two positions: +1 and −1, at a certain temperature , interacting through the IsingErnst Ising
Ernst Ising was a German physicist, who is best remembered for the development of the Ising model. He was a professor of physics at Bradley University until his retirement in 1976.-Life:Ernst Ising was born in Cologne in 1900...
classical Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
:
where the sum is extended over the pairs of nearest neighbours and
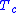is a coupling constant, which we will consider to be fixed. There is a certain temperature, called the Curie temperature or critical temperature, below which the system presents ferromagnetic long range order. Above it, it is paramagnetic and is apparently disordered.At temperature zero, the system may only take one global sign, either +1 or -1. At higher temperatures, but below
, the state is still globally magnetized, but clusters of the opposite sign appears. As the temperature increases, these clusters start to contain smaller clusters themselves, in a typical Russian dolls picture. Their typical size, called the correlation length, grows with temperature until it diverges at 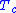. This means that the whole system is such a cluster, and there is no global magnetization. Above that temperature, the system is globally disordered, but with ordered clusters within it, whose size is again called correlation length, but it is now decreasing with temperature. At infinite temperature, it is again zero, with the system fully disordered.Divergences at the critical point
The correlation length diverges at the critical point: as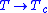, 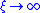. This divergence poses no physical problem. Other physical observables diverge at this point, leading to some confusion at the beginning.The most important is susceptibility
Susceptibility
*In physics, the susceptibility of a material or substance describes its response to an applied field. There are many kinds of susceptibilities, for example:These two susceptibilities are particular examples of a linear response function;...
. Let us apply a very small magnetic field to the
system in the critical point. A very small magnetic field is not able to magnetize a large coherent cluster, but with these fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
clusters the picture changes. It affects easily the smallest size clusters, since they have a nearly paramagnetic behaviour. But this change, in its turn, affects the next-scale clusters, and the perturbation climbs the ladder until the whole system changes radically. Thus, critical systems are very sensitive to small changes in the environment.
Other observables, such as the specific heat, may also diverge at this point. All these divergences stem from that of the correlation length.
Critical exponents and universality
As we approach the critical point, these diverging observables behave as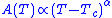 for some exponent where, typically, the value of the exponent α is the same above and below Tc. These exponents are called critical exponents and are robust observables. Even more, they take the same values for very different physical systems. This intriguing phenomenon, called universalityUniversality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
, is explained, qualitatively and also quantitatively, by the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.
Critical dynamics
Critical phenomena may also appear for dynamic quantities, not only for static ones. In fact, the divergence of the characteristic time of a system is directly related to the divergence of the thermal correlation length by the introduction of a dynamical exponent z and the relation . The voluminous static universality class of a system splits into different, less voluminous dynamic universality classes with different values of zbut a common static critical behaviour, and by approaching the critical point one may observe all kinds of slowing-down phenomena.
Ergodicity breaking
ErgodicityErgodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
is the assumption that a system, at a given temperature, explores the full phase space, just each state takes different probabilities. In an Ising ferromagnet below
this does not happen. If , never mind how close they are, the system has chosen a global magnetization, and the phase space is divided into two regions. From one of them it is impossible to reach the other, unless a magnetic field is applied, or temperature is raised above 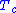.See also superselection sector
Superselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
Mathematical tools
The main mathematical tools to study critical points are renormalization groupRenormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
, which takes advantage of the Russian dolls picture to explain universality and predict numerically the critical exponents, and Variational perturbation theory, which converts divergent perturbation expansions into convergent strong-coupling expansions relevant to critical phenomena. In two-dimensional systems, Conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
is a powerful tool which has discovered many new properties of 2D critical systems, employing the fact that scale invariance, along with a few other requisites, leads to an infinite symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
.
Applications
Applications arise in physics and chemistry, but also in sciences as the sociologySociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
. For example, it is natural to describe a system of two political parties by an Ising model. Thereby, at a transition between one majority to the other one the above-mentioned critical phenomena may appear.
See also
- Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
- Critical pointCritical point (thermodynamics)In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
- Critical exponentCritical exponentCritical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
- Critical opalescenceCritical opalescenceCritical opalescence is a phenomenon which arises in the region of a continuous, or second-order, phase transition. Originally reported by Thomas Andrews in 1869 for the liquid-gas transition in carbon dioxide, many other examples have been discovered since. The phenomenon is most commonly...
- Variational perturbation theory
- Conformal field theoryConformal field theoryA conformal field theory is a quantum field theory that is invariant under conformal transformations...
- ErgodicityErgodicityIn mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
- Self-organized criticalitySelf-organized criticalityIn physics, self-organized criticality is a property of dynamical systems which have a critical point as an attractor. Their macroscopic behaviour thus displays the spatial and/or temporal scale-invariance characteristic of the critical point of a phase transition, but without the need to tune...
- Rushbrooke inequalityRushbrooke inequalityIn statistical mechanics, the Rushbrooke inequality relates the critical exponents of a magnetic system which exhibits a first-order phase transition in the thermodynamic limit for non-zero temperature T....
- Widom scalingWidom scalingWidom scaling is a hypothesis in statistical mechanics regarding the free energy of a magnetic system near its critical point which leads to the critical exponents becoming no longer independent so that they can be parameterized in terms of two values...