
Widom scaling
Encyclopedia
Widom scaling is a hypothesis in statistical mechanics
regarding the free energy
of a magnetic system near its critical point
which leads to the critical exponent
s becoming no longer independent so that they can be parameterized in terms of two values. The hypothesis can be seen to arise as a natural consequence of the block-spin renormalization procedure, when the block size is chosen to be of the same size as the correlation length.
Widom scaling is an example of universality
.
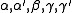 and
and 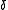 are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
 , for
, for 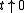
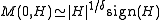 , for
, for 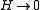
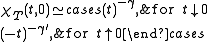
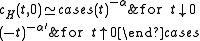
where
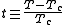 measures the temperature relative to the critical point.
measures the temperature relative to the critical point.
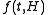 , in
, in 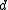 dimensions, can be written as the sum of a slowly varying regular part
dimensions, can be written as the sum of a slowly varying regular part  and a singular part
and a singular part 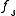 , with the singular part being a scaling function, ie, a homogeneous function
, with the singular part being a scaling function, ie, a homogeneous function
, so that
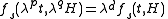
Then taking the partial derivative
with respect to H and the form of M(t,H) gives
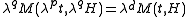
Setting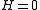 and
and 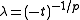 in the preceding equation yields
in the preceding equation yields
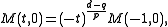 for
for 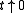
Comparing this with the definition of yields its value,
yields its value,
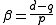
Similarly, putting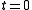 and
and 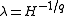 into the scaling relation for M yields
into the scaling relation for M yields

Applying the expression for the isothermal susceptibility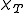 in terms of M to the scaling relation yields
in terms of M to the scaling relation yields
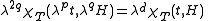
Setting H=0 and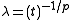 for
for 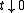 (resp.
(resp. 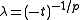 for
for 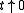 ) yields
) yields
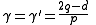
Similarly for the expression for specific heat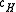 in terms of M to the scaling relation yields
in terms of M to the scaling relation yields
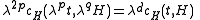
Taking H=0 and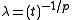 for
for 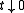 (or
(or 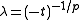 for
for  yields
yields
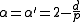
As a consequence of Widom scaling, not all critical exponents are independent but they can be parameterized by two numbers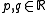 with the relations expressed as
with the relations expressed as
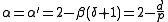
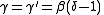
The relations are experimentally well verified for magnetic systems and fluids.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
regarding the free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
of a magnetic system near its critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
which leads to the critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s becoming no longer independent so that they can be parameterized in terms of two values. The hypothesis can be seen to arise as a natural consequence of the block-spin renormalization procedure, when the block size is chosen to be of the same size as the correlation length.
Widom scaling is an example of universality
Universality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
.
Definitions
The critical exponents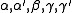 and
and 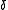 are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows , for
, for 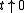
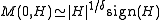 , for
, for 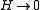
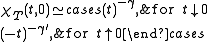
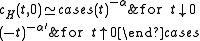
where
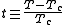 measures the temperature relative to the critical point.
measures the temperature relative to the critical point.Derivation
The scaling hypothesis is that near the critical point, the free energy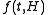 , in
, in 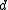 dimensions, can be written as the sum of a slowly varying regular part
dimensions, can be written as the sum of a slowly varying regular part  and a singular part
and a singular part 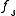 , with the singular part being a scaling function, ie, a homogeneous function
, with the singular part being a scaling function, ie, a homogeneous functionHomogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
, so that
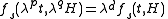
Then taking the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to H and the form of M(t,H) gives
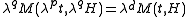
Setting
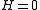 and
and 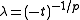 in the preceding equation yields
in the preceding equation yields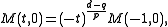 for
for 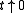
Comparing this with the definition of
 yields its value,
yields its value,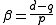
Similarly, putting
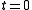 and
and 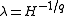 into the scaling relation for M yields
into the scaling relation for M yields
Applying the expression for the isothermal susceptibility
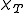 in terms of M to the scaling relation yields
in terms of M to the scaling relation yields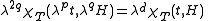
Setting H=0 and
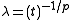 for
for 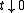 (resp.
(resp. 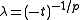 for
for 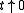 ) yields
) yields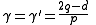
Similarly for the expression for specific heat
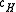 in terms of M to the scaling relation yields
in terms of M to the scaling relation yields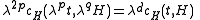
Taking H=0 and
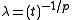 for
for 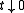 (or
(or 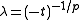 for
for  yields
yields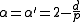
As a consequence of Widom scaling, not all critical exponents are independent but they can be parameterized by two numbers
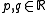 with the relations expressed as
with the relations expressed as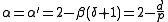
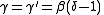
The relations are experimentally well verified for magnetic systems and fluids.

