Mellin inversion theorem
Encyclopedia
In mathematics
, the Mellin inversion formula (named after Hjalmar Mellin
) tells us conditions under
which the inverse Mellin transform
, or equivalently the inverse two-sided Laplace transform
, are defined and recover the transformed function.
If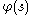
is analytic in the strip 
,
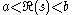and if it tends to zero uniformly with increasing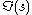
for any real value c between a and b, with its integral along such a line converging absolutely, then if
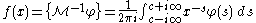
we have that
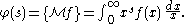
Conversely, suppose f(x) is piecewise continuous on the positive real numbers, taking a value halfway between the limit values at any jump discontinuities, and suppose the integral
is absolutely convergent when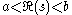
. Then f is recoverable via the inverse Mellin transform from its Mellin transform 
.
We may strengthen the boundedness condition on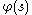
if
f(x) is continuous. If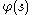
is analytic in the strip 
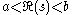, and if 
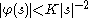, where K is a positive constant, then f(x) as defined by the inversion integral exists and is continuous; moreover the Mellin transform of f is 
for at least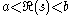 
.
On the other hand, if we are willing to accept an original f which is a
generalized function
, we may relax the boundedness condition on
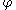to
simply make it of polynomial growth in any closed strip contained in the open strip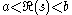
.
We may also define a Banach space
version of this theorem. If we call by
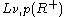the weighted Lp space
of complex valued functions f on the positive reals such that
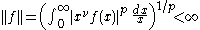
where ν and p are fixed real numbers with p>1, then if f(x)
is in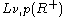
with 
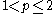, then
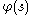belongs to 
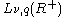with 
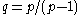and
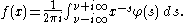
Here functions, identical everywhere except on a set of measure zero, are identified.
Since the two-sided Laplace transform can be defined as
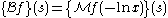
these theorems can be immediately applied to it also.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Mellin inversion formula (named after Hjalmar Mellin
Hjalmar Mellin
Robert Hjalmar Mellin was a Finnish mathematician and functional theorist.He studied at the University of Helsinki and later in Berlin under Karl Weierstrass. He is most noted as the developer of the integral transform known as the Mellin transform...
) tells us conditions under
which the inverse Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
, or equivalently the inverse two-sided Laplace transform
Two-sided Laplace transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform, the Mellin transform, and the ordinary or one-sided Laplace transform...
, are defined and recover the transformed function.
If
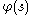is analytic in the strip 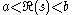,and if it tends to zero uniformly with increasing
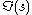for any real value c between a and b, with its integral along such a line converging absolutely, then if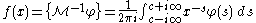we have that
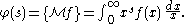
Conversely, suppose f(x) is piecewise continuous on the positive real numbers, taking a value halfway between the limit values at any jump discontinuities, and suppose the integral
is absolutely convergent when
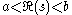. Then f is recoverable via the inverse Mellin transform from its Mellin transform .We may strengthen the boundedness condition on
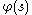iff(x) is continuous. If
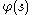is analytic in the strip 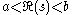, and if 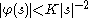, where K is a positive constant, then f(x) as defined by the inversion integral exists and is continuous; moreover the Mellin transform of f is for at least 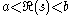.On the other hand, if we are willing to accept an original f which is a
generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
, we may relax the boundedness condition on
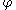tosimply make it of polynomial growth in any closed strip contained in the open strip
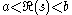.We may also define a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
version of this theorem. If we call by
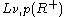the weighted Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of complex valued functions f on the positive reals such that
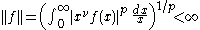
where ν and p are fixed real numbers with p>1, then if f(x)
is in
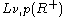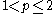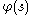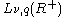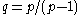with , then belongs to with and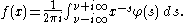Here functions, identical everywhere except on a set of measure zero, are identified.
Since the two-sided Laplace transform can be defined as
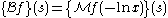
these theorems can be immediately applied to it also.
External links
- Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.
- Philippe Flajolet, Xavier Gourdon, Philippe Dumas, Mellin Transforms and Asymptotics: Harmonic sums.