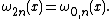Cunningham function
Encyclopedia
In statistics
, the Cunningham function or Pearson–Cunningham function ωm,n(x) is a generalisation of a special function introduced by and studied in the form here by . It can be defined in terms of the confluent hypergeometric function
U, by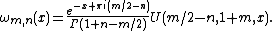
The function was studied by Cunningham in the context of a multivariate generalisation of the Edgeworth expansion for approximating a probability density function
based on its (joint) moments
. In a more general context, the function is related to the solution of the constant-coefficient diffusion equation, in one or more dimensions.
The function ωm,n(x) is a solution of the differential equation for X:
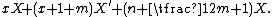
The special function studied by Pearson is given, in his notation by,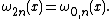
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Cunningham function or Pearson–Cunningham function ωm,n(x) is a generalisation of a special function introduced by and studied in the form here by . It can be defined in terms of the confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
U, by
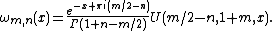
The function was studied by Cunningham in the context of a multivariate generalisation of the Edgeworth expansion for approximating a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
based on its (joint) moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
. In a more general context, the function is related to the solution of the constant-coefficient diffusion equation, in one or more dimensions.
The function ωm,n(x) is a solution of the differential equation for X:
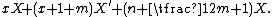
The special function studied by Pearson is given, in his notation by,