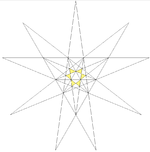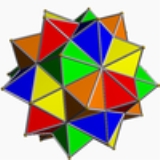
Compound of five octahedra
Encyclopedia
| Compound of five octahedra | |||||||
|---|---|---|---|---|---|---|---|
 |
|||||||
| Type | Regular compound | ||||||
| Index | UC17, W23 | ||||||
| Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... (As a compound) |
5 octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... : F = 40, E = 60, V = 30 |
||||||
| Dual compound Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
Compound of five cubes Compound of five cubes This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra.... |
||||||
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (Ih) |
||||||
| Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H... restricting to one constituent |
pyritohedral Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group... (Th) |
||||||
|
|||||||
This polyhedron can be seen as either a polyhedral stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
or a compound. This compound was first described by Edmund Hess
Edmund Hess
Edmund Hess was a German mathematician who discovered several regular polytopes.- References :* Regular Polytopes, , Dover edition, ISBN 0-486-61480-8...
in 1876.
As a stellation
It is the second stellationStellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and given as Wenninger model index 23.
It can be constructed by a rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
with rhombic-based pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
s added to all the faces, as shown by the five colored model image.
As a compound
It can also be seen as a polyhedral compoundPolyhedral compound
A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
of five octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
arranged in icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(Ih).
It shares its edges and half of its triangular faces with the compound of five tetrahemihexahedra
Compound of five tetrahemihexahedra
A compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It is chiral with icosahedral symmetry .- Related polyhedra :...
.
 Compound of five octahedra |
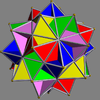 Compound of five tetrahemihexahedra Compound of five tetrahemihexahedra A compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It is chiral with icosahedral symmetry .- Related polyhedra :... |
As a facetting
It is a facettingFacetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
of the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, as shown below:
At left only one octahedron is shown; all five are shown at right.
See also
- Compound of three octahedraCompound of three octahedraIn mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized...
- Compound of four octahedraCompound of four octahedraThis uniform polyhedron compound is a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis .- Cartesian coordinates :Cartesian coordinates for the...
- Compound of ten octahedraCompound of ten octahedraThese uniform polyhedron compounds are symmetric arrangements of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron...
- Compound of twenty octahedraCompound of twenty octahedraThis uniform polyhedron compound is a symmetric arrangement of 20 octahedra . It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.- Related polyhedra :...
External links
- MathWorld: Octahedron5-Compound
- Paper Model Compound of Five Octahedra
- VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
model: http://www.interocitors.com/polyhedra/UCs/17%__5_Octahedra.wrl