
Smallest circle problem
Encyclopedia
The smallest circle problem or minimum covering circle problem is a mathematical problem
of computing the smallest circle
that contains all of a given set of point
s in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere
problem, is to compute the smallest n-sphere that contains all of a given set of points. The smallest circle problem was initially proposed by the English mathematician James Joseph Sylvester
in 1857.
The smallest circle problem in the plane is an example of a facility location
problem in which the location of a new facility must be chosen to provide service to a number of customers, minimizing the farthest distance that any customer must travel to reach the new facility.
Welzl proposed a simple randomized algorithm for the
minimum covering circle problem that runs in expected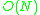 time, based on a linear programming
time, based on a linear programming
algorithm of Raimund Seidel
.
The algorithm is recursive, and takes as arguments two sets of points S and Q; it computes the smallest enclosing circle of the union of S and Q, as long as every point of Q is one of the boundary points of the eventual smallest enclosing circle. Thus, the original smallest enclosing circle problem can be solved by calling the algorithm with S equal to the set of points to be enclosed and Q equal to the empty set
; as the algorithm calls itself recursively, it will enlarge the set Q passed into the recursive calls until it includes all the boundary points of the circle.
The algorithm processes the points of S in a random order, maintaining as it does the set P of processed points and the smallest circle that encloses the union of P and Q. At each step, it tests whether the next point r to be processed belongs to this circle; if it does not, the algorithm replaces the enclosing circle by the result of a recursive call of the algorithm on the sets P and Q+r. Whether the circle was replaced or not, r is then included in the set P. Processing each point, therefore, consists of testing in constant time whether the point belongs to a single circle and possibly performing a recursive call to the algorithm. It can be shown that the ith point to be processed has probability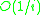 of generating a recursive call, and therefore that the overall time is linear.
of generating a recursive call, and therefore that the overall time is linear.
Mathematical problem
A mathematical problem is a problem that is amenable to being represented, analyzed, and possibly solved, with the methods of mathematics. This can be a real-world problem, such as computing the orbits of the planets in the solar system, or a problem of a more abstract nature, such as Hilbert's...
of computing the smallest circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
that contains all of a given set of point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere
Bounding sphere
In mathematics, given a non-empty set of objects of finite extension in n-dimensional space, for example a set of points, a bounding sphere, enclosing sphere or enclosing ball for that set is an n-dimensional solid sphere containing all of these objects.In the plane the terms bounding or enclosing...
problem, is to compute the smallest n-sphere that contains all of a given set of points. The smallest circle problem was initially proposed by the English mathematician James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
in 1857.
The smallest circle problem in the plane is an example of a facility location
Facility location
Facility location, also known as location analysis, is a branch of operations research and computational geometry concerning itself with mathematical modeling and solution of problems concerning optimal placement of facilities in order to minimize transportation costs, avoid placing hazardous...
problem in which the location of a new facility must be chosen to provide service to a number of customers, minimizing the farthest distance that any customer must travel to reach the new facility.
Characterization
Most of the geometric approaches for the problem look for points that lie on the boundary of the minimum circle and are based on the following simple facts:- The minimum covering circle is unique.
- The minimum covering circle of a set S can be determined by at most three points in S which lie on the boundary of the circle. If it is determined by only two points, then the line segment joining those two points must be a diameter of the minimum circle. If it is determined by three points, then the triangle consisting of those three points is not obtuse.
Linear-time solutions
As Megiddo showed, the minimum enclosing circle can be found in linear time, and the same linear time bound also applies to the smallest enclosing sphere in Euclidean spaces of any constant dimension.Welzl proposed a simple randomized algorithm for the
minimum covering circle problem that runs in expected
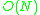 time, based on a linear programming
time, based on a linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
algorithm of Raimund Seidel
Raimund Seidel
Raimund G. Seidel is a professor of computer scientist at the Universität des Saarlandes and an expert in computational geometry.Seidel was born in Graz, Austria, and studied with Hermann Maurer at the Graz University of Technology. He received his Ph.D. in 1987 from Cornell University under the...
.
The algorithm is recursive, and takes as arguments two sets of points S and Q; it computes the smallest enclosing circle of the union of S and Q, as long as every point of Q is one of the boundary points of the eventual smallest enclosing circle. Thus, the original smallest enclosing circle problem can be solved by calling the algorithm with S equal to the set of points to be enclosed and Q equal to the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
; as the algorithm calls itself recursively, it will enlarge the set Q passed into the recursive calls until it includes all the boundary points of the circle.
The algorithm processes the points of S in a random order, maintaining as it does the set P of processed points and the smallest circle that encloses the union of P and Q. At each step, it tests whether the next point r to be processed belongs to this circle; if it does not, the algorithm replaces the enclosing circle by the result of a recursive call of the algorithm on the sets P and Q+r. Whether the circle was replaced or not, r is then included in the set P. Processing each point, therefore, consists of testing in constant time whether the point belongs to a single circle and possibly performing a recursive call to the algorithm. It can be shown that the ith point to be processed has probability
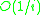 of generating a recursive call, and therefore that the overall time is linear.
of generating a recursive call, and therefore that the overall time is linear.Other algorithms
Prior to Megiddo's result showing that the smallest circle problem may be solved in linear time, several effective algorithms of higher (worst case) complexity appeared in the literature. A naive algorithm solves the problem in time O(n4) by testing the circles determined by all pairs and triples of points.- An algorithm of Chrystal and Peirce applies a local optimization strategy that maintains two points on the boundary of an enclosing circle and repeatedly shrinks the circle, replacing the pair of boundary points, until an optimal circle is found. Chakraborty and Chaudhuri propose a linear-time method for selecting a suitable initial circle and a pair of boundary points on that circle. Each step of the algorithm includes as one of the two boundary points a new vertex of the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
, so if the hull has h vertices this method can be implemented to run in time O(nh). - Elzinga and Hearn described an algorithm which maintains a covering circle for a subset of the points. At each step, a point not covered by the current sphere is used to find a larger sphere that covers a new subset of points, including the point found. Although its worst case running time is O(h3n), the authors report that it ran in linear time in their experiments. The complexity of the method has been analyzed by Drezner and Shelah. Both Fortran and C codes are available, see the ORSEP article.
- The smallest sphere problem can be formulated as a quadratic program defined by a system of linear constraints with a convex quadratic objective function. Therefore, any feasible direction algorithm can give the solution of the problem. Hearn and Vijay proved that the feasible direction approach chosen by Jacobsen is equivalent to the Chrystal–Peirce algorithm.
- The dual to this quadratic program may also be formulated explicitly; an algorithm of Lawson can be described in this way as a primal dual algorithm.
- Shamos and Hoey proposed an O(n log n) time algorithm for the problem based on the observation that the center of the smallest enclosing circle must be a vertex of the farthest-point Voronoi diagramVoronoi diagramIn mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
of the input point set.
Weighted variants of the problem
The weighted version of the minimum covering circle problem takes as input a set of points in a Euclidean space, each with weights; the goal is to find a single point that minimizes the maximum weighted distance to any point. The original minimum covering circle problem can be recovered by setting all weights to the same number. As with the unweighted problem, the weighted problem may be solved in linear time in any space of bounded dimension, using approaches closely related to bounded dimension linear programming algorithms, although slower algorithms are again frequent in the literature. The weighted version of the Elzinga-Hearn algorithm is available via the ORSEP article mentioned above.External links
- Bernd Gärtner's smallest enclosing ball code
- Miniball open source project for smallest enclosing balls
- http://www.sonycsl.co.jp/person/nielsen/PT/seb/seb.html F. Nielsen and R. Nock, Approximating Smallest Enclosing Balls, 2004

