Cellular model - AbsoluteAstronomy.com

Creating a cellular model has been a particularly challenging task of systems biology

Systems biology

Systems biology is a term used to describe a number of trends in bioscience research, and a movement which draws on those trends. Proponents describe systems biology as a biology-based inter-disciplinary study field that focuses on complex interactions in biological systems, claiming that it uses...

and mathematical biology

Mathematical biology

Mathematical and theoretical biology is an interdisciplinary scientific research field with a range of applications in biology, medicine and biotechnology...

.
It involves developing efficient algorithms, data structures, visualization

Biological data visualization

Biology Data Visualization is a branch of bioinformatics concerned with the application of computer graphics, scientific visualization, and information visualization to different areas of the life sciences. This includes visualization of sequences, genomes, alignments, phylogenies, macromolecular...

and communication tools to orchestrate the integration of large quantities of biological data with the goal of computer modeling.

It is also directly associated with bioinformatics

Bioinformatics

Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...

, computational biology

Computational biology

Computational biology involves the development and application of data-analytical and theoretical methods, mathematical modeling and computational simulation techniques to the study of biological, behavioral, and social systems...

and Artificial life

Artificial life

Artificial life is a field of study and an associated art form which examine systems related to life, its processes, and its evolution through simulations using computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American computer scientist, in 1986...

.

It involves the use of computer simulation

Computer simulation

A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...

s of the many cellular

Cell (biology)

The cell is the basic structural and functional unit of all known living organisms. It is the smallest unit of life that is classified as a living thing, and is often called the building block of life. The Alberts text discusses how the "cellular building blocks" move to shape developing embryos....

subsystems such as the networks of metabolites

Metabolic network

A metabolic network is the complete set of metabolic and physical processes that determine the physiological and biochemical properties of a cell...

and enzyme

Enzyme

Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...

s which comprise metabolism

Metabolism

Metabolism is the set of chemical reactions that happen in the cells of living organisms to sustain life. These processes allow organisms to grow and reproduce, maintain their structures, and respond to their environments. Metabolism is usually divided into two categories...

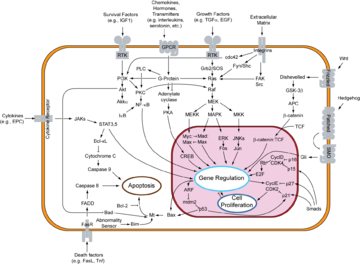
, signal transduction

Signal transduction

Signal transduction occurs when an extracellular signaling molecule activates a cell surface receptor. In turn, this receptor alters intracellular molecules creating a response...

pathways and gene regulatory network

Gene regulatory network

A gene regulatory network or genetic regulatory network is a collection of DNA segments in a cell whichinteract with each other indirectly and with other substances in the cell, thereby governing the rates at which genes in the network are transcribed into mRNA.In general, each mRNA molecule goes...

s to both analyze and visualize the complex connections of these cellular processes.

The complex network of biochemical reaction/transport processes and their spatial organization make the development of a predictive model of a living cell a grand challenge for the 21st century.

Overview

The eukaryotic cell cycle

Cell cycle

The cell cycle, or cell-division cycle, is the series of events that takes place in a cell leading to its division and duplication . In cells without a nucleus , the cell cycle occurs via a process termed binary fission...

is very complex and is one of the most studied topics, since its misregulation leads to cancer

Cancer

Cancer , known medically as a malignant neoplasm, is a large group of different diseases, all involving unregulated cell growth. In cancer, cells divide and grow uncontrollably, forming malignant tumors, and invade nearby parts of the body. The cancer may also spread to more distant parts of the...

s.
It is possibly a good example of a mathematical model as it deals with simple calculus but gives valid results. Two research groups have produced several models of the cell cycle simulating several organisms. They have recently produced a generic eukaryotic cell cycle model which can represent a particular eukaryote depending on the values of the parameters, demonstrating that the idiosyncrasies of the individual cell cycles are due to different protein concentrations and affinities, while the underlying mechanisms are conserved (Csikasz-Nagy et al., 2006).

By means of a system of ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

s these models show the change in time (dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

) of the protein inside a single typical cell; this type of model is called a deterministic process (whereas a model describing a statistical distribution of protein concentrations in a population of cells is called a stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

).

To obtain these equations an iterative series of steps must be done: first the several models and observations are combined to form a consensus diagram and the appropriate kinetic laws are chosen to write the differential equations, such as rate kinetics

Reaction rate

The reaction rate or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place...

for stoichiometric reactions, Michaelis-Menten kinetics

Michaelis-Menten kinetics

In biochemistry, Michaelis–Menten kinetics is one of the simplest and best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating...

for enzyme substrate reactions and Goldbeter–Koshland kinetics for ultrasensitive transcription factors, afterwards the parameters of the equations (rate constants, enzyme efficiency coefficients and Michealis constants) must be fitted to match observations; when they cannot be fitted the kinetic equation is revised and when that is not possible the wiring diagram is modified. The parameters are fitted and validated using observations of both wild type and mutants, such as protein half-life and cell size.

In order to fit the parameters the differential equations need to be studied. This can be done either by simulation or by analysis.

In a simulation, given a starting vector (list of the values of the variables), the progression of the system is calculated by solving the equations at each time-frame in small increments.

In analysis, the proprieties of the equations are used to investigate the behavior of the system depending of the values of the parameters and variables. A system of differential equations can be represented as a vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

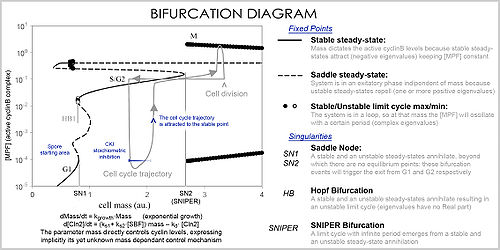
, where each vector described the change (in concentration of two or more protein) determining where and how fast the trajectory (simulation) is heading. Vector fields can have several special points: a stable point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

, called a sink, that attracts in all directions (forcing the concentrations to be at a certain value), an unstable point, either a source or a saddle point

Saddle point

In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...

which repels (forcing the concentrations to change away from a certain value), and a limit cycle, a closed trajectory towards which several trajectories spiral towards (making the concentrations oscillate).
A better representation which can handle the large number of variables and parameters is called a bifurcation diagram

Bifurcation diagram

In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...

(bifurcation theory

Bifurcation theory

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...

): the presence of these special steady-state points at certain values of a parameter (e.g. mass) is represented by a point and once the parameter passes a certain value, a qualitative change occurs, called a bifurcation, in which the nature of the space changes, with profound consequences for the protein concentrations: the cell cycle has phases (partially corresponding to G1 and G2) in which mass, via a stable point, controls cyclin levels, and phases (S and M phases) in which the concentrations change independently, but once the phase has changed at a bifurcation event (cell cycle checkpoint

Cell cycle checkpoint

Cell cycle checkpoints are control mechanisms that ensure the fidelity of cell division in eukaryotic cells. These checkpoints verify whether the processes at each phase of the cell cycle have been accurately completed before progression into the next phase...

), the system cannot go back to the previous levels since at the current mass the vector field is profoundly different and the mass cannot be reversed back through the bifurcation event, making a checkpoint irreversible. In particular the S and M checkpoints are regulated by means of special bifurcations called a Hopf bifurcation

Hopf bifurcation

In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...

and an infinite period bifurcation.

Molecular level simulations

E-Cell Project aims "to make precise whole cell simulation at the molecular level possible".

Projects

Multiple projects are in progress.

Karyote - Indiana University
Indiana University
Indiana University is a multi-campus public university system in the state of Indiana, United States. Indiana University has a combined student body of more than 100,000 students, including approximately 42,000 students enrolled at the Indiana University Bloomington campus and approximately 37,000...
E-Cell Project
Virtual Cell - University of Connecticut Health Center
University of Connecticut Health Center
The University of Connecticut Health Center includes the , School of Dental Medicine, , the UConn Medical Group, UConn Health Partners and . Founded in 1961, the Health Center pursues a mission of providing outstanding health care education in an environment of exemplary patient care, research and...
Silicon Cell

Overview

Molecular level simulations

Projects

See also