
Capacity of a set
Encyclopedia
In mathematics
, the capacity of a set in Euclidean space
is a measure of that set's "size". Unlike, say, Lebesgue measure
, which measures a set's volume
or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance
of the set: the total charge a set can hold while maintaining a given potential energy
. The potential energy is computed with respect to an idealized ground at infinity for the harmonic or Newtonian capacity, and with respect to a surface for the condenser capacity.
in 1950: for a detailed account, see reference .
al hypersurface
in n-dimensional Euclidean space ℝn, n ≥ 3; K will denote the n-dimensional compact
(i.e., closed
and bounded
) set of which Σ is the boundary
. Let S be another (n − 1)-dimensional hypersurface that encloses Σ: in reference to its origins in electromagnetism
, the pair (Σ, S) is known as a condenser
. The condenser capacity of Σ relative to S, denoted C(Σ, S) or cap(Σ, S), is given by the surface integral
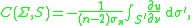
where:
C(Σ, S) can be equivalently defined by the volume integral
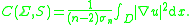
The condenser capacity also has a variational characterization
: C(Σ, S) is the infimum
of the Dirichlet's energy functional

over all continuously-differentiable functions
v on D with v(x) = 1 on Σ and v(x) = 0 on S.
ally, the harmonic capacity of K, the region bounded by Σ, can be found by taking the condenser capacity of Σ with respect to infinity. More precisely, let u be the harmonic function in the complement of K satisfying u = 1 on Σ and u(x) → 0 as x → ∞. Thus u is the Newtonian potential
of the simple layer Σ. Then the harmonic capacity (also known as the Newtonian capacity) of K, denoted C(K) or cap(K), is then defined by
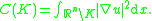
If S is a rectifiable hypersurface completely enclosing K, then the harmonic capacity can be equivalently rewritten as the integral over S of the outward normal derivative of u:
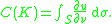
The harmonic capacity can also be understood as a limit of the condenser capacity. To wit, let Sr denote the sphere
of radius r about the origin in ℝn. Since K is bounded, for sufficiently large r, Sr will enclose K and (Σ, Sr) will form a condenser pair. The harmonic capacity is then the limit
as r tends to infinity:
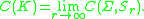
The harmonic capacity is a mathematically abstract version of the electrostatic capacity of the conductor K and is always non-negative and finite: 0 ≤ C(K) < +∞.
achieving particular boundary values, given above, can be extended to other energy functionals in the calculus of variations
.
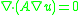
are minimizers of the associated energy functional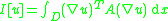
subject to appropriate boundary conditions.
The capacity of a set E with respect to a domain D containing E is defined as the infimum
of the energy over all continuously-differentiable functions
v on D with v(x) = 1 on E; and v(x) = 0 on the boundary of D.
The minimum energy is achieved by a function known as the capacitary potential of E with respect to D, and it solves the obstacle problem
on D with the obstacle function provided by the indicator function of E. The capacitary potential is alternately characterized as the unique solution of the equation with the appropriate boundary conditions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the capacity of a set in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is a measure of that set's "size". Unlike, say, Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, which measures a set's volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance
Capacitance
In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
of the set: the total charge a set can hold while maintaining a given potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
. The potential energy is computed with respect to an idealized ground at infinity for the harmonic or Newtonian capacity, and with respect to a surface for the condenser capacity.
Historical note
The notion of capacity of a set and of "capacitable" set was introduced by Gustave ChoquetGustave Choquet
Gustave Choquet was a French mathematician.Choquet was born in Solesmes, Nord. His contributions include work in functional analysis, potential theory, topology and measure theory...
in 1950: for a detailed account, see reference .
Condenser capacity
Let Σ be a closed, smooth, (n − 1)-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in n-dimensional Euclidean space ℝn, n ≥ 3; K will denote the n-dimensional compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
(i.e., closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
) set of which Σ is the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
. Let S be another (n − 1)-dimensional hypersurface that encloses Σ: in reference to its origins in electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, the pair (Σ, S) is known as a condenser
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
. The condenser capacity of Σ relative to S, denoted C(Σ, S) or cap(Σ, S), is given by the surface integral
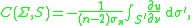
where:
- u is the unique harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
defined on the region D between Σ and S with the boundary conditions u(x) = 1 on Σ and u(x) = 0 on S; - S′ is any intermediate surface between Σ and S;
- ν is the outward unit normal fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
to S′ and
- is the normal derivative of u across S′; and
- σn = 2πn⁄2 ⁄ Γ(n ⁄ 2) is the surface area of the unit sphereUnit sphereIn mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
in ℝn.
- σn = 2πn⁄2 ⁄ Γ(n ⁄ 2) is the surface area of the unit sphere
C(Σ, S) can be equivalently defined by the volume integral
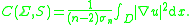
The condenser capacity also has a variational characterization
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
: C(Σ, S) is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the Dirichlet's energy functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...

over all continuously-differentiable functions
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
v on D with v(x) = 1 on Σ and v(x) = 0 on S.
Harmonic/Newtonian capacity
HeuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
ally, the harmonic capacity of K, the region bounded by Σ, can be found by taking the condenser capacity of Σ with respect to infinity. More precisely, let u be the harmonic function in the complement of K satisfying u = 1 on Σ and u(x) → 0 as x → ∞. Thus u is the Newtonian potential
Newtonian potential
In mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...
of the simple layer Σ. Then the harmonic capacity (also known as the Newtonian capacity) of K, denoted C(K) or cap(K), is then defined by
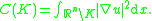
If S is a rectifiable hypersurface completely enclosing K, then the harmonic capacity can be equivalently rewritten as the integral over S of the outward normal derivative of u:
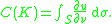
The harmonic capacity can also be understood as a limit of the condenser capacity. To wit, let Sr denote the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius r about the origin in ℝn. Since K is bounded, for sufficiently large r, Sr will enclose K and (Σ, Sr) will form a condenser pair. The harmonic capacity is then the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as r tends to infinity:
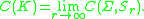
The harmonic capacity is a mathematically abstract version of the electrostatic capacity of the conductor K and is always non-negative and finite: 0 ≤ C(K) < +∞.
Generalizations
The characterization of the capacity of a set as the minimum of an energy functionalEnergy functional
Energy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...
achieving particular boundary values, given above, can be extended to other energy functionals in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
Divergence form elliptic operators
Solutions to a uniformly elliptic partial differential equation with divergence form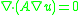
are minimizers of the associated energy functional
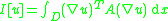
subject to appropriate boundary conditions.
The capacity of a set E with respect to a domain D containing E is defined as the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the energy over all continuously-differentiable functions
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
v on D with v(x) = 1 on E; and v(x) = 0 on the boundary of D.
The minimum energy is achieved by a function known as the capacitary potential of E with respect to D, and it solves the obstacle problem
Obstacle problem
The obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problems. The problem is to find the equilibrium position of an elastic membrane whose boundary is held fixed, and which is constrained to lie above a given obstacle...
on D with the obstacle function provided by the indicator function of E. The capacitary potential is alternately characterized as the unique solution of the equation with the appropriate boundary conditions.


