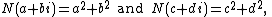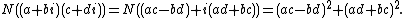Brahmagupta-Fibonacci identity
Encyclopedia
In algebra
, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed
under multiplication. Specifically:
For example,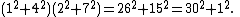
The identity is a special case (n = 1) of Lagrange's identity, and is first found in Diophantus. Brahmagupta proved and used a more general identity, equivalent to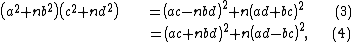
showing that the set of all numbers of the form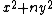
is closed under multiplication.
Both (1) and (2) can be verified by expanding
each side of the equation. Also, (2) can be obtained from (1), or (1) from (2), by changing b to −b.
This identity holds in both the ring of integers
and the ring of rational numbers
, and more generally in any commutative ring
.
In the integer
case this identity finds applications in number theory
for example when used in conjunction with one of Fermat's theorems it proves that the product of a square and any number of primes of the form 4n + 1 is also a sum of two squares.
's Arithmetica (III, 19).
The identity was rediscovered by Brahmagupta
(598–668), an Indian mathematician and astronomer, who generalized it and used it in his study of what is now erroneously called Pell's equation
. His Brahmasphutasiddhanta
was translated from Sanskrit
into Arabic
by Mohammad al-Fazari, and was subsequently translated into Latin
in 1126. The identity later appeared in Fibonacci
's Book of Squares
in 1225.
is an analogous identity involving four squares instead of two that is related to quaternions. There is a similar eight-square identity
derived from the Cayley numbers which has connections to Bott periodicity.
s, this identity is equivalent to the multiplication property for absolute values of complex numbers namely that:
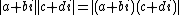
since
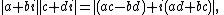
by squaring both sides
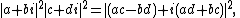
and by the definition of absolute value,
s, the identity may be interpreted as the statement that the norm
in the field
Q(i) is multiplicative. That is, we have
and also
Therefore the identity is saying that
, namely x2 − Ny2 = 1. Using the identity in the more general form
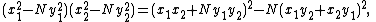
he was able to "compose" triples (x1, y1, k1) and (x2, y2, k2) that were solutions of x2 − Ny2 = k, to generate the new triple
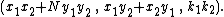
Not only did this give a way to generate infinitely many solutions to x2 − Ny2 = 1 starting with one solution, but also, by dividing such a composition by k1k2, integer or "nearly integer" solutions could often be obtained. The general method for solving the Pell equation given by Bhaskara II in 1150, namely the chakravala (cyclic) method
, was also based on this identity.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under multiplication. Specifically:
For example,
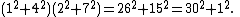
The identity is a special case (n = 1) of Lagrange's identity, and is first found in Diophantus. Brahmagupta proved and used a more general identity, equivalent to
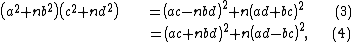
showing that the set of all numbers of the form
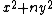is closed under multiplication.Both (1) and (2) can be verified by expanding
Polynomial expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...
each side of the equation. Also, (2) can be obtained from (1), or (1) from (2), by changing b to −b.
This identity holds in both the ring of integers
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and the ring of rational numbers
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, and more generally in any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
In the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
case this identity finds applications in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
for example when used in conjunction with one of Fermat's theorems it proves that the product of a square and any number of primes of the form 4n + 1 is also a sum of two squares.
History
The identity is first found in DiophantusDiophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
's Arithmetica (III, 19).
The identity was rediscovered by Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
(598–668), an Indian mathematician and astronomer, who generalized it and used it in his study of what is now erroneously called Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
. His Brahmasphutasiddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
was translated from Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
into Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
by Mohammad al-Fazari, and was subsequently translated into Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
in 1126. The identity later appeared in Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
's Book of Squares
The Book of Squares
The Book of Squares, in the original Latin is a book on algebra by Leonardo Fibonacci, published in 1225. Fibonacci's identity, establishing that the set of all sums of two squares is closed under multiplication, appears in it. The book anticipated the works of later mathematicians like Fermat and...
in 1225.
Related identities
Euler's four-square identityEuler's four-square identity
In mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:=\,...
is an analogous identity involving four squares instead of two that is related to quaternions. There is a similar eight-square identity
Degen's eight-square identity
In mathematics, Degen's eight-square identity establishes that the product of two numbers, each of which being a sum of eight squares, is itself a sum of eight squares...
derived from the Cayley numbers which has connections to Bott periodicity.
Relation to complex numbers
If a, b, c, and d are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, this identity is equivalent to the multiplication property for absolute values of complex numbers namely that:
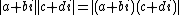
since
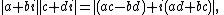
by squaring both sides
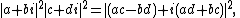
and by the definition of absolute value,
Interpretation via norms
In the case that the variables a, b, c, and d are rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, the identity may be interpreted as the statement that the norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
in the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Q(i) is multiplicative. That is, we have
and also
Therefore the identity is saying that
Application to Pell's equation
In its original context, Brahmagupta applied his discovery to the solution of Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, namely x2 − Ny2 = 1. Using the identity in the more general form
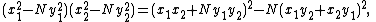
he was able to "compose" triples (x1, y1, k1) and (x2, y2, k2) that were solutions of x2 − Ny2 = k, to generate the new triple
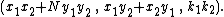
Not only did this give a way to generate infinitely many solutions to x2 − Ny2 = 1 starting with one solution, but also, by dividing such a composition by k1k2, integer or "nearly integer" solutions could often be obtained. The general method for solving the Pell equation given by Bhaskara II in 1150, namely the chakravala (cyclic) method
Chakravala method
The chakravala method is a cyclic algorithm to solve indeterminate quadratic equations, including Pell's equation. It is commonly attributed to Bhāskara II, although some attribute it to Jayadeva...
, was also based on this identity.
External links
- http://planetmath.org/encyclopedia/BrahmaguptasIdentity.htmlBrahmagupta's identity at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
] - Brahmagupta Identity on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Brahmagupta-Fibonacci identity
- A Collection of Algebraic Identities