
Bohr–van Leeuwen theorem
Encyclopedia
The Bohr–van Leeuwen theorem is a theorem in the field of statistical mechanics
. The theorem shows that when statistical mechanics and classical mechanics
are applied consistently, the thermal average of the magnetization
is always zero. This makes magnetism in solids solely a quantum mechanical effect and means that classical physics cannot account for diamagnetism
, paramagnetism
or ferromagnetism
.
in 1911 in his doctoral dissertation and was later rediscovered by Hendrika Johanna van Leeuwen in her doctoral thesis in 1919. In 1932, van Vleck
formalized and expanded upon Bohr's initial theorem in a book he wrote on electric and magnetic susceptibilities. The significance of this discovery is that classical physics does not allow for such things as paramagnetism
, diamagnetism
and ferromagnetism
and thus quantum physics and relativity
are needed to explain the magnetic events. This result, "perhaps the most deflationary publication of all time," may have contributed to Bohr's development of a quasi-classical theory of the hydrogen atom
in 1913.
in a given temperature and field, and the system is allowed time to return to equilibrium after a field is applied, then there will be no magnetization.
The probability that the system will be in a given state of motion is predicted by Maxwell-Boltzmann statistics to be proportional to , where is the energy of the system,
is the energy of the system,  is the Boltzmann constant, and
is the Boltzmann constant, and  is the temperature
is the temperature
. This energy is equal to the kinetic energy
(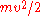 for a particle with mass
for a particle with mass  and speed
and speed  ) and the potential energy
) and the potential energy
.
The magnetic field does not contribute to the potential energy. The Lorentz force
on a particle with charge
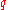 and velocity
and velocity
 is
is
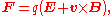
where is the electric field
is the electric field
and is the magnetic flux density. The rate of work
is the magnetic flux density. The rate of work
done is and does not depend on
and does not depend on  . Therefore, the energy does not depend on the magnetic field, so the distribution of motions does not depend on the magnetic field.
. Therefore, the energy does not depend on the magnetic field, so the distribution of motions does not depend on the magnetic field.
In zero field, there will be no net motion of charged particles because the system is not able to rotate. There will therefore be an average magnetic moment of zero. Since the distribution of motions does not depend on the magnetic field, the moment in thermal equilibrium remains zero in any magnetic field.
 electrons. This is appropriate, since most of the magnetism in a solid is carried by electrons, and the proof is easily generalized to more than one type of charged particle. Each electron has a negative charge
electrons. This is appropriate, since most of the magnetism in a solid is carried by electrons, and the proof is easily generalized to more than one type of charged particle. Each electron has a negative charge  and mass
and mass  . If its position is
. If its position is  and velocity is
and velocity is  , it produces a current
, it produces a current
 and a magnetic moment
and a magnetic moment

The above equation shows that the magnetic moment is a linear function of the position coordinates, so the total magnetic moment in a given direction must be a linear function of the form
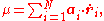
where the dot represents a time derivative and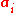 are vector coefficients depending on the position coordinates
are vector coefficients depending on the position coordinates 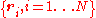 .
.
Maxwell-Boltzmann statistics gives the probability that the nth particle has momentum and coordinate
and coordinate  as
as
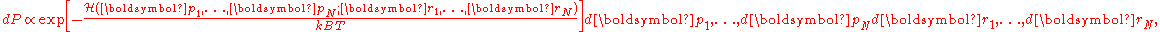
where is the Hamiltonian, the total energy of the system.
is the Hamiltonian, the total energy of the system.
The thermal average of any function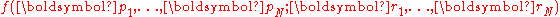 of these generalized coordinates
of these generalized coordinates
is then
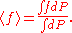
In the presence of a magnetic field,
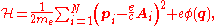
where is the magnetic vector potential and
is the magnetic vector potential and 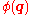 is the electric scalar potential.
is the electric scalar potential.
For each particle the components of the momentum and position
and position 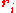 are related by the equations of Hamiltonian mechanics
are related by the equations of Hamiltonian mechanics
:
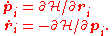
Therefore,
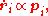
so the moment is a linear function of the momenta
is a linear function of the momenta 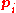 .
.
The thermally averaged moment,
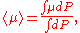
is the sum of terms proportional to integrals of the form

where represents one of the moment coordinates. The integrand is an odd function of
represents one of the moment coordinates. The integrand is an odd function of 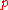 , so it vanishes. Therefore,
, so it vanishes. Therefore, 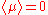 .
.
for the plasma element." Electromechanics
and electrical engineering
also see practical benefit from the Bohr–van Leeuwen theorem.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The theorem shows that when statistical mechanics and classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
are applied consistently, the thermal average of the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
is always zero. This makes magnetism in solids solely a quantum mechanical effect and means that classical physics cannot account for diamagnetism
Diamagnetism
Diamagnetism is the property of an object which causes it to create a magnetic field in opposition to an externally applied magnetic field, thus causing a repulsive effect. Specifically, an external magnetic field alters the orbital velocity of electrons around their nuclei, thus changing the...
, paramagnetism
Paramagnetism
Paramagnetism is a form of magnetism whereby the paramagnetic material is only attracted when in the presence of an externally applied magnetic field. In contrast with this, diamagnetic materials are repulsive when placed in a magnetic field...
or ferromagnetism
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
.
History
What is today known as the Bohr–van Leeuwen theorem was discovered by Niels BohrNiels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
in 1911 in his doctoral dissertation and was later rediscovered by Hendrika Johanna van Leeuwen in her doctoral thesis in 1919. In 1932, van Vleck
John Hasbrouck van Vleck
John Hasbrouck Van Vleck was an American physicist and mathematician, co-awarded the 1977 Nobel Prize in Physics, for his contributions to the understanding of the behavior of electrons in magnetic solids....
formalized and expanded upon Bohr's initial theorem in a book he wrote on electric and magnetic susceptibilities. The significance of this discovery is that classical physics does not allow for such things as paramagnetism
Paramagnetism
Paramagnetism is a form of magnetism whereby the paramagnetic material is only attracted when in the presence of an externally applied magnetic field. In contrast with this, diamagnetic materials are repulsive when placed in a magnetic field...
, diamagnetism
Diamagnetism
Diamagnetism is the property of an object which causes it to create a magnetic field in opposition to an externally applied magnetic field, thus causing a repulsive effect. Specifically, an external magnetic field alters the orbital velocity of electrons around their nuclei, thus changing the...
and ferromagnetism
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
and thus quantum physics and relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
are needed to explain the magnetic events. This result, "perhaps the most deflationary publication of all time," may have contributed to Bohr's development of a quasi-classical theory of the hydrogen atom
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
in 1913.
An intuitive proof
The Bohr–van Leeuwen theorem applies to an isolated system that cannot rotate (an isolated star could start rotating if exposed to a field). If, in addition, there is only one state of thermal equilibriumThermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
in a given temperature and field, and the system is allowed time to return to equilibrium after a field is applied, then there will be no magnetization.
The probability that the system will be in a given state of motion is predicted by Maxwell-Boltzmann statistics to be proportional to , where
 is the energy of the system,
is the energy of the system,  is the Boltzmann constant, and
is the Boltzmann constant, and  is the temperature
is the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. This energy is equal to the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(
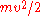 for a particle with mass
for a particle with mass  and speed
and speed  ) and the potential energy
) and the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
.
The magnetic field does not contribute to the potential energy. The Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
on a particle with charge
Charge
Charge or charged may refer to:* Charge , illegal contact by pushing or moving into another player's torso* Charge , a six-note trumpet or bugle piece denoting the call to rush forward...
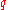 and velocity
and velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
 is
is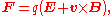
where
 is the electric field
is the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and
 is the magnetic flux density. The rate of work
is the magnetic flux density. The rate of workWork
Work may refer to:Human labor:* Employment* House work* Labor , measure of the work done by human beings* Manual labor, physical work done by people* Wage labor, in which a worker sells their labor and an employer buys it...
done is
 and does not depend on
and does not depend on  . Therefore, the energy does not depend on the magnetic field, so the distribution of motions does not depend on the magnetic field.
. Therefore, the energy does not depend on the magnetic field, so the distribution of motions does not depend on the magnetic field.In zero field, there will be no net motion of charged particles because the system is not able to rotate. There will therefore be an average magnetic moment of zero. Since the distribution of motions does not depend on the magnetic field, the moment in thermal equilibrium remains zero in any magnetic field.
A more formal proof
We will consider, for simplicity, a system with electrons. This is appropriate, since most of the magnetism in a solid is carried by electrons, and the proof is easily generalized to more than one type of charged particle. Each electron has a negative charge
electrons. This is appropriate, since most of the magnetism in a solid is carried by electrons, and the proof is easily generalized to more than one type of charged particle. Each electron has a negative charge  and mass
and mass  . If its position is
. If its position is  and velocity is
and velocity is  , it produces a current
, it produces a currentElectric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
 and a magnetic moment
and a magnetic momentMagnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...

The above equation shows that the magnetic moment is a linear function of the position coordinates, so the total magnetic moment in a given direction must be a linear function of the form
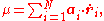
where the dot represents a time derivative and
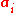 are vector coefficients depending on the position coordinates
are vector coefficients depending on the position coordinates 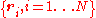 .
.Maxwell-Boltzmann statistics gives the probability that the nth particle has momentum
 and coordinate
and coordinate  as
as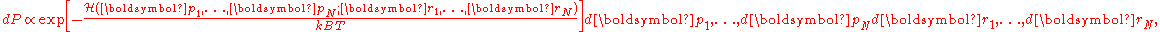
where
 is the Hamiltonian, the total energy of the system.
is the Hamiltonian, the total energy of the system.The thermal average of any function
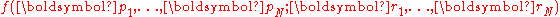 of these generalized coordinates
of these generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
is then
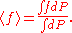
In the presence of a magnetic field,
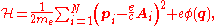
where
 is the magnetic vector potential and
is the magnetic vector potential and 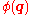 is the electric scalar potential.
is the electric scalar potential.For each particle the components of the momentum
 and position
and position 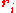 are related by the equations of Hamiltonian mechanics
are related by the equations of Hamiltonian mechanicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
:
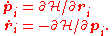
Therefore,
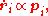
so the moment
 is a linear function of the momenta
is a linear function of the momenta 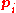 .
.The thermally averaged moment,
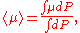
is the sum of terms proportional to integrals of the form

where
 represents one of the moment coordinates. The integrand is an odd function of
represents one of the moment coordinates. The integrand is an odd function of 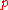 , so it vanishes. Therefore,
, so it vanishes. Therefore, 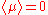 .
.Applications of the Bohr–van Leeuwen theorem
The Bohr–van Leeuwen theorem is useful in several applications including plasma physics, "All these references base their discussion of the Bohr–van Leeuwen theorem on Niels Bohr's physical model, in which perfectly reflecting walls are necessary to provide the currents that cancel the net contribution from the interior of an element of plasma, and result in zero net diamagnetismfor the plasma element." Electromechanics
Electromechanics
In engineering, electromechanics combines the sciences of electromagnetism, of electrical engineering and mechanics. Mechanical engineering in this context refers to the larger discipline which includes chemical engineering, and other related disciplines. Electrical engineering in this context...
and electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
also see practical benefit from the Bohr–van Leeuwen theorem.

