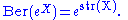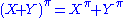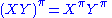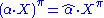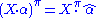Supermatrix
Encyclopedia
In mathematics
and theoretical physics
, a supermatrix is a Z2-graded analog of an ordinary matrix
. Specifically, a supermatrix is a 2×2 block matrix
with entries in a superalgebra
(or superring). The most important examples are those with entries in a commutative superalgebra (such as a Grassmann algebra) or an ordinary field
(thought of as a purely even commutative superalgebra).
Supermatrices arise in the study of super linear algebra where they appear as the coordinate representations of a linear transformation
s between finite-dimensional super vector space
s or free supermodule
s. They have important applications in the field of supersymmetry
.
(assumed to be unital and associative). Often one requires R be supercommutative as well (for essentially the same reasons as in the ungraded case).
Let p, q, r, and s be nonnegative integers. A supermatrix of dimension (r|s)×(p|q) is a matrix
with entries in R that is partitioned into a 2×2 block structure
with r+s total rows and p+q total columns (so that the submatrix X00 has dimensions r×p and X11 has dimensions s×q). An ordinary (ungraded) matrix can be thought of as a supermatrix for which q and s are both zero.
A square supermatrix is one for which (r|s) = (p|q). This means that not only is the unpartitioned matrix X square, but the diagonal blocks X00 and X11 are as well.
An even supermatrix is one for which diagonal blocks (X00 and X11) consist solely of even elements of R (i.e. homogeneous elements of parity 0) and the off-diagonal blocks (X01 and X10) consist solely of odd elements of R.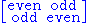
An odd supermatrix is one for the reverse holds: the diagonal blocks are odd and the off-diagonal blocks are even.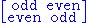
If the scalars R are purely even there are no nonzero odd elements, so the even supermatices are the block diagonal ones and the odd supermatrices are the off-diagonal ones.
A supermatrix is homogeneous if it is either even or odd. The parity, |X|, of a nonzero homogeneous supermatrix X is 0 or 1 according to whether it is even or odd. Every supermatrix can be written uniquely as the sum of an even supermatrix and an odd one.
Let Mr|s×p|q(R) denote the set of all supermatrices over R with dimension (r|s)×(p|q). This set forms a supermodule
over R under supermatrix addition and scalar multiplication. In particular, if R is a superalgebra over a field K then Mr|s×p|q(R) forms a super vector space
over K.
Let Mp|q(R) denote the set of all square supermatices over R with dimension (p|q)×(p|q). This set forms a superring under supermatrix addition and multiplication. Furthermore, if R is a commutative superalgebra, then supermatrix multiplication is a bilinear operation, so that Mp|q(R) forms a superalgebra over R.
to obtain a supermatrix of the same dimension. The addition can be performed blockwise since the blocks have compatible sizes. It is easy to see that the sum of two even supermatrices is even and the sum of two odd supermatrices is odd.
to obtain a matrix of dimension (r|s)×(k|l). The multiplication can be performed at the block level in the obvious manner: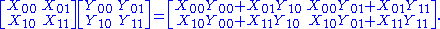
Note that the blocks of the product supermatrix Z = XY are given by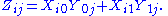
If X and Y are homogeneous with parities |X| and |Y| then XY is homogeneous with parity |X| + |Y|. That is, the product of two even or two odd supermatrices is even while the product of an even and odd supermatrix is odd.
for supermatrices is different than the ungraded case due to the presence of odd elements in R. Let X be a supermatrix. Left scalar multiplication by α ∈ A is defined by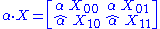
where the internal scalar multiplications are the ordinary ungraded ones and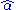
denotes the grade involution in A. This is given on homogeneous elements by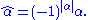
Right scalar multiplication by α is defined analogously: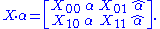
If α is even then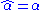
and both of these operations are the same as the ungraded versions. If α and X are homogeneous then α·X and X·α are both homogeneous with parity |α| + |X|. Furthermore, if R is supercommutative then one has
s (or free module
s). Likewise, supermatrices can be thought of as the coordinate representations of linear maps between super vector space
s (or free supermodules). There is an important difference in the graded case, however. A homomorphism from one super vector space to another is, by definition, one that preserves the grading (i.e. maps even elements to even elements and odd elements to odd elements). The coordinate representation of such a transformation is always an even supermatrix. Odd supermatrices correspond to linear transformations that reverse the grading. General supermatrices represent an arbitrary ungraded linear transformation. Such transformations are still important in the graded case, although less so than the graded (even) transformations.
A supermodule
M over a superalgebra
R is free if it has a free homogeneous basis. If such a basis consists of p even elements and q odd elements, then M is said to have rank p|q. If R is supercommutative, the rank is independent of the choice of basis, just as in the ungraded case.
Let Rp|q be the space of column supervectors—supermatrices of dimension (p|q)×(1|0). This is naturally a right R-supermodule, called the right coordinate space. A supermatrix T of dimension (r|s)×(p|q) can then be thought of as a right R-linear map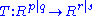
where the action of T on Rp|q is just supermatrix multiplication (this action is not generally left R-linear which is why we think of Rp|q as a right supermodule).
Let M be free right R-supermodule of rank p|q and let N be a free right R-supermodule of rank r|s. Let (ei) be a free basis for M and let (fk) be a free basis for N. Such a choice of bases is equivalent to a choice of isomorphisms from M to Rp|q and from N to Rr|s. Any (ungraded) linear map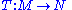
can be written as a (r|s)×(p|q) supermatrix relative to the chosen bases. The components of the associated supermatrix are determined by the formula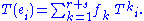
The block decomposition of a supermatrix T corresponds to the decomposition of M and N into even and odd submodules:
. Let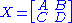
be a homogeneous (r|s)×(p|q) supermatrix. The supertranspose of X is the (p|q)×(r|s) supermatrix
where At denotes the ordinary transpose of A. This can be extended to arbitrary supermatrices by linearity. Unlike the ordinary transpose, the supertranspose is not generally an involution, but rather has order 4. Applying the supertranspose twice to a supermatrix X gives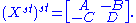
If R is supercommutative, the supertranspose satisfies the identity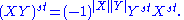
be a (r|s)×(p|q) supermatrix. The parity transpose of X is the (s|r)×(q|p) supermatrix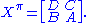
That is, the (i,j) block of the transposed matrix is the (1−i,1−j) block of the original matrix.
The parity transpose operation obeys the identities
as well as
where st denotes the supertranspose operation.
of a square supermatrix is the Z2-graded analog of the trace
. It is defined on homogeneous supermatrices by the formula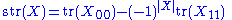
where tr denotes the ordinary trace.
If R is supercommutative, the supertrace satisfies the identity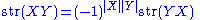
for homogeneous supermatrices X and Y.
(or superdeterminant) of a square supermatrix is the Z2-graded analog of the determinant
. The Berezinian is only well-defined on even, invertible supermatrices over a commutative superalgebra R. In this case it is given by the formula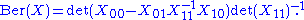
where det denotes the ordinary determinant (of square matrices with entries in the commutative algebra R0).
The Berezinian satisfies similar properties to the ordinary determinant. In particular, it is multiplicative and invariant under the supertranspose. It is related to the supertrace by the formula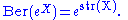
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a supermatrix is a Z2-graded analog of an ordinary matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Specifically, a supermatrix is a 2×2 block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
with entries in a superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
(or superring). The most important examples are those with entries in a commutative superalgebra (such as a Grassmann algebra) or an ordinary field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(thought of as a purely even commutative superalgebra).
Supermatrices arise in the study of super linear algebra where they appear as the coordinate representations of a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s between finite-dimensional super vector space
Super vector space
In mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
s or free supermodule
Supermodule
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics....
s. They have important applications in the field of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
.
Definitions and notation
Let R be a fixed superalgebraSuperalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
(assumed to be unital and associative). Often one requires R be supercommutative as well (for essentially the same reasons as in the ungraded case).
Let p, q, r, and s be nonnegative integers. A supermatrix of dimension (r|s)×(p|q) is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries in R that is partitioned into a 2×2 block structure
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
with r+s total rows and p+q total columns (so that the submatrix X00 has dimensions r×p and X11 has dimensions s×q). An ordinary (ungraded) matrix can be thought of as a supermatrix for which q and s are both zero.
A square supermatrix is one for which (r|s) = (p|q). This means that not only is the unpartitioned matrix X square, but the diagonal blocks X00 and X11 are as well.
An even supermatrix is one for which diagonal blocks (X00 and X11) consist solely of even elements of R (i.e. homogeneous elements of parity 0) and the off-diagonal blocks (X01 and X10) consist solely of odd elements of R.
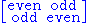
An odd supermatrix is one for the reverse holds: the diagonal blocks are odd and the off-diagonal blocks are even.
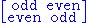
If the scalars R are purely even there are no nonzero odd elements, so the even supermatices are the block diagonal ones and the odd supermatrices are the off-diagonal ones.
A supermatrix is homogeneous if it is either even or odd. The parity, |X|, of a nonzero homogeneous supermatrix X is 0 or 1 according to whether it is even or odd. Every supermatrix can be written uniquely as the sum of an even supermatrix and an odd one.
Algebraic structure
Supermatrices of compatible dimensions can be added or multiplied just as for ordinary matrices. These operations are exactly the same as the ordinary ones with the restriction that they are defined only when the blocks have compatible dimensions. One can also multiply supermatrices by elements of R (on the left or right), however, this operation differs from the ungraded case due to the presence of odd elements in R.Let Mr|s×p|q(R) denote the set of all supermatrices over R with dimension (r|s)×(p|q). This set forms a supermodule
Supermodule
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics....
over R under supermatrix addition and scalar multiplication. In particular, if R is a superalgebra over a field K then Mr|s×p|q(R) forms a super vector space
Super vector space
In mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
over K.
Let Mp|q(R) denote the set of all square supermatices over R with dimension (p|q)×(p|q). This set forms a superring under supermatrix addition and multiplication. Furthermore, if R is a commutative superalgebra, then supermatrix multiplication is a bilinear operation, so that Mp|q(R) forms a superalgebra over R.
Addition
Two supermatrices of dimension (r|s)×(p|q) can be added just as in the ungraded caseMatrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
to obtain a supermatrix of the same dimension. The addition can be performed blockwise since the blocks have compatible sizes. It is easy to see that the sum of two even supermatrices is even and the sum of two odd supermatrices is odd.
Multiplication
One can multiply a supermatrix with dimensions (r|s)×(p|q) by a supermatrix with dimensions (p|q)×(k|l) as in the ungraded caseMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
to obtain a matrix of dimension (r|s)×(k|l). The multiplication can be performed at the block level in the obvious manner:
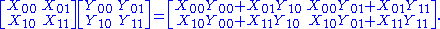
Note that the blocks of the product supermatrix Z = XY are given by
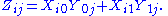
If X and Y are homogeneous with parities |X| and |Y| then XY is homogeneous with parity |X| + |Y|. That is, the product of two even or two odd supermatrices is even while the product of an even and odd supermatrix is odd.
Scalar multiplication
Scalar multiplicationScalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
for supermatrices is different than the ungraded case due to the presence of odd elements in R. Let X be a supermatrix. Left scalar multiplication by α ∈ A is defined by
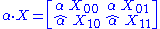
where the internal scalar multiplications are the ordinary ungraded ones and
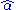denotes the grade involution in A. This is given on homogeneous elements by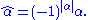Right scalar multiplication by α is defined analogously:
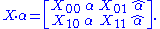
If α is even then
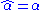and both of these operations are the same as the ungraded versions. If α and X are homogeneous then α·X and X·α are both homogeneous with parity |α| + |X|. Furthermore, if R is supercommutative then one hasAs linear transformations
Ordinary matrices can be thought of as the coordinate representations of linear maps between vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s (or free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s). Likewise, supermatrices can be thought of as the coordinate representations of linear maps between super vector space
Super vector space
In mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
s (or free supermodules). There is an important difference in the graded case, however. A homomorphism from one super vector space to another is, by definition, one that preserves the grading (i.e. maps even elements to even elements and odd elements to odd elements). The coordinate representation of such a transformation is always an even supermatrix. Odd supermatrices correspond to linear transformations that reverse the grading. General supermatrices represent an arbitrary ungraded linear transformation. Such transformations are still important in the graded case, although less so than the graded (even) transformations.
A supermodule
Supermodule
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics....
M over a superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
R is free if it has a free homogeneous basis. If such a basis consists of p even elements and q odd elements, then M is said to have rank p|q. If R is supercommutative, the rank is independent of the choice of basis, just as in the ungraded case.
Let Rp|q be the space of column supervectors—supermatrices of dimension (p|q)×(1|0). This is naturally a right R-supermodule, called the right coordinate space. A supermatrix T of dimension (r|s)×(p|q) can then be thought of as a right R-linear map
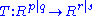
where the action of T on Rp|q is just supermatrix multiplication (this action is not generally left R-linear which is why we think of Rp|q as a right supermodule).
Let M be free right R-supermodule of rank p|q and let N be a free right R-supermodule of rank r|s. Let (ei) be a free basis for M and let (fk) be a free basis for N. Such a choice of bases is equivalent to a choice of isomorphisms from M to Rp|q and from N to Rr|s. Any (ungraded) linear map
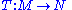
can be written as a (r|s)×(p|q) supermatrix relative to the chosen bases. The components of the associated supermatrix are determined by the formula
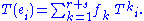
The block decomposition of a supermatrix T corresponds to the decomposition of M and N into even and odd submodules:
Operations
Many operations on ordinary matrices can be generalized to supermatrices, although the generalizations are not always obvious or straightforward.Supertranspose
The supertranspose of a supermatrix is the Z2-graded analog of the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
. Let
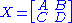
be a homogeneous (r|s)×(p|q) supermatrix. The supertranspose of X is the (p|q)×(r|s) supermatrix
where At denotes the ordinary transpose of A. This can be extended to arbitrary supermatrices by linearity. Unlike the ordinary transpose, the supertranspose is not generally an involution, but rather has order 4. Applying the supertranspose twice to a supermatrix X gives
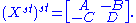
If R is supercommutative, the supertranspose satisfies the identity
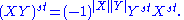
Parity transpose
The parity transpose of a supermatrix is a new operation without an ungraded analog. Letbe a (r|s)×(p|q) supermatrix. The parity transpose of X is the (s|r)×(q|p) supermatrix
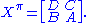
That is, the (i,j) block of the transposed matrix is the (1−i,1−j) block of the original matrix.
The parity transpose operation obeys the identities
as well as
where st denotes the supertranspose operation.
Supertrace
The supertraceSupertrace
In the theory of superalgebras, if A is a commutative superalgebra, V is a free right A-supermodule and T is an endomorphism from V to itself, then the supertrace of T, str is defined by the following trace diagram:...
of a square supermatrix is the Z2-graded analog of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
. It is defined on homogeneous supermatrices by the formula
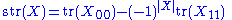
where tr denotes the ordinary trace.
If R is supercommutative, the supertrace satisfies the identity
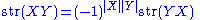
for homogeneous supermatrices X and Y.
Berezinian
The BerezinianBerezinian
In mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin...
(or superdeterminant) of a square supermatrix is the Z2-graded analog of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. The Berezinian is only well-defined on even, invertible supermatrices over a commutative superalgebra R. In this case it is given by the formula
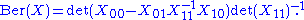
where det denotes the ordinary determinant (of square matrices with entries in the commutative algebra R0).
The Berezinian satisfies similar properties to the ordinary determinant. In particular, it is multiplicative and invariant under the supertranspose. It is related to the supertrace by the formula