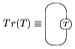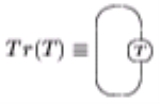
Supertrace
Encyclopedia
In the theory of superalgebra
s, if A is a commutative superalgebra, V is a free right A-supermodule
and T is an endomorphism
from V to itself, then the supertrace of T, str(T) is defined by the following trace diagram
:
More concretely, if we write out T in block matrix
form after the decomposition into even and odd subspaces as follows,
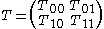
then the supertrace
Let us show that the supertrace does not depend on a basis.
Suppose e1, ..., ep are the even basis vectors and ep+1, ..., ep+q are the odd basis vectors. Then, the components of T, which are elements of A, are defined as
The grading of Tij is the sum of the gradings of T, ei, ej mod 2.
A change of basis to e1', ..., ep', e(p+1)', ..., e(p+q)' is given by the supermatrix
and the inverse supermatrix
where of course, AA−1 = A−1A = 1 (the identity).
We can now check explicitly that the supertrace is basis independent. In the case where T is even, we have
In the case where T is odd, we have
The ordinary trace is not basis independent, so the appropriate trace to use in the Z2-graded setting is the supertrace.
The supertrace satisfies the property
for all T1, T2 in End(V). In particular, the supertrace of a supercommutator is zero.
In fact, one can define a supertrace more generally for any associative superalgebra E over a commutative superalgebra A as a linear map tr: E -> A which vanishes on supercommutators. Such a supertrace is not uniquely defined; it can always at least be modified by multiplication by an element of A.
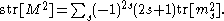
In anomaly-free theories where only renormalizable terms appear in the superpotential, the above supertrace can be shown to vanish, even when supersymmetry is spontaneously broken.
The contribution to the effective potential arising at one loop (sometimes referred to as the Coleman-Weinberg potential) can also be written in terms of a supertrace. If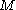
is the mass matrix for a given theory, the one-loop potential can be written as
where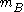
and 
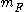are the respective tree-level mass matrices for the separate bosonic and fermionic degrees of freedom in the theory and 
is a cutoff scale.
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
s, if A is a commutative superalgebra, V is a free right A-supermodule
Supermodule
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics....
and T is an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
from V to itself, then the supertrace of T, str(T) is defined by the following trace diagram
Trace diagram
In mathematics, trace diagrams are a graphical means of performing computations in linear and multilinear algebra. They can be represented as graphs in which some edges are labeled by matrices. The simplest trace diagrams represent the trace and determinant of a matrix...
:
More concretely, if we write out T in block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
form after the decomposition into even and odd subspaces as follows,
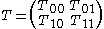
then the supertrace
- str(T) = the ordinary trace of T0 0 − the ordinary trace of T11.
Let us show that the supertrace does not depend on a basis.
Suppose e1, ..., ep are the even basis vectors and ep+1, ..., ep+q are the odd basis vectors. Then, the components of T, which are elements of A, are defined as
The grading of Tij is the sum of the gradings of T, ei, ej mod 2.
A change of basis to e1', ..., ep', e(p+1)', ..., e(p+q)' is given by the supermatrix
Supermatrix
In mathematics and theoretical physics, a supermatrix is a Z2-graded analog of an ordinary matrix. Specifically, a supermatrix is a 2×2 block matrix with entries in a superalgebra...
and the inverse supermatrix
where of course, AA−1 = A−1A = 1 (the identity).
We can now check explicitly that the supertrace is basis independent. In the case where T is even, we have
In the case where T is odd, we have
The ordinary trace is not basis independent, so the appropriate trace to use in the Z2-graded setting is the supertrace.
The supertrace satisfies the property
for all T1, T2 in End(V). In particular, the supertrace of a supercommutator is zero.
In fact, one can define a supertrace more generally for any associative superalgebra E over a commutative superalgebra A as a linear map tr: E -> A which vanishes on supercommutators. Such a supertrace is not uniquely defined; it can always at least be modified by multiplication by an element of A.
Physics Applications
In supersymmetric quantum field theories, in which the action integral is invariant under a set of symmetry transformations (known as supersymmetry transformations) whose algebras are superalgebras, the supertrace has a variety of applications. In such a context, the supertrace of the mass matrix for the theory can be written as a sum over spins of the traces of the mass matrices for particles of different spin: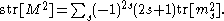In anomaly-free theories where only renormalizable terms appear in the superpotential, the above supertrace can be shown to vanish, even when supersymmetry is spontaneously broken.
The contribution to the effective potential arising at one loop (sometimes referred to as the Coleman-Weinberg potential) can also be written in terms of a supertrace. If
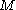is the mass matrix for a given theory, the one-loop potential can be written aswhere
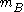and 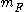are the respective tree-level mass matrices for the separate bosonic and fermionic degrees of freedom in the theory and is a cutoff scale.