Midrange
Encyclopedia
In statistics
, the mid-range or mid-extreme of a set of statistical data values is the arithmetic mean
of the maximum and minimum values in a data set
, or:
As such, it is a measure of central tendency
.
The midrange is highly sensitive to outliers and ignores all but two data points. It is therefore a very non-robust statistic (having a breakdown point of 0, meaning that a single observation can change it arbitrarily), and it is rarely used in statistical analysis.
The midhinge
is the 25% trimmed
mid-range, and is more robust, having a breakdown point of 25%.
estimator
of μ, given a small sample of a sufficiently platykurtic distribution, but it is inefficient for mesokurtic distributions, such as the normal.
For example, for a continuous uniform distribution with unknown maximum and minimum, the mid-range is the UMVU estimator for the mean. The sample maximum and sample minimum, together with sample size, are a sufficient statistic for the population maximum and minimum – the distribution of other samples, conditional on a given maximum and minimum, is just the uniform distribution between the maximum and minimum and thus add no information. Thus the mid-range, which is an unbiased and sufficient estimator of the population mean, is in fact the UMVU:
using the sample mean just adds noise based on the uninformative distribution of points within this range.
Conversely, for the normal distribution, the sample mean is the UMVU estimator of the mean. Thus for platykurtic distributions, which can often be thought of as between a uniform distribution and a normal distribution, the informativeness of the middle sample points versus the extrema values varies from "equal" for normal to "uninformative" for uniform, and for different distributions, one or the other (or some combination thereof) may be most efficient.
A limited amount of experimental work on the efficiency of measures of central tendency for small samples by William D. Vinson reveals the following facts, where γ2 is the coefficient of excess kurtosis
, defined as γ2 = (μ4/(μ2)²) − 3.
This generalization holds for sample sizes (n) from 4 to 20.
When n = 3, there can be no modified mean, and the mean is the most efficient measure of central tendency for values of γ2 form 2.0 to 6.0 as well as from −0.8 to 2.0.
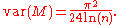
For a sample of size n from the standard Laplace distribution, the mid-range M is unbiased, and has a variance given by
and, in particular, the variance does not decrease to zero as the sample size grows.
For a sample of size n from a zero-centred uniform distribution
, the mid-range M is unbiased, nM has an asymptotic distribution
which is a Laplace distribution.
and the median
minimizes the average absolute deviation, the midrange minimizes the maximum deviation (defined as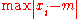
): it is a solution to a variational problem.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the mid-range or mid-extreme of a set of statistical data values is the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the maximum and minimum values in a data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
, or:
As such, it is a measure of central tendency
Central tendency
In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
.
The midrange is highly sensitive to outliers and ignores all but two data points. It is therefore a very non-robust statistic (having a breakdown point of 0, meaning that a single observation can change it arbitrarily), and it is rarely used in statistical analysis.
The midhinge
Midhinge
In statistics, the midhinge is the average of the first and third quartiles and is thus a measure of location.Equivalently, it is the 25% trimmed mid-range; it is an L-estimator....
is the 25% trimmed
Trimmed estimator
Given an estimator, a trimmed estimator is obtained by excluding some of the extreme values. This is generally done to obtain a more robust statistic: the extreme values are considered outliers....
mid-range, and is more robust, having a breakdown point of 25%.
Efficiency
Despite its drawbacks, in some cases it is useful: the midrange is a highly efficientEfficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of μ, given a small sample of a sufficiently platykurtic distribution, but it is inefficient for mesokurtic distributions, such as the normal.
For example, for a continuous uniform distribution with unknown maximum and minimum, the mid-range is the UMVU estimator for the mean. The sample maximum and sample minimum, together with sample size, are a sufficient statistic for the population maximum and minimum – the distribution of other samples, conditional on a given maximum and minimum, is just the uniform distribution between the maximum and minimum and thus add no information. Thus the mid-range, which is an unbiased and sufficient estimator of the population mean, is in fact the UMVU:
using the sample mean just adds noise based on the uninformative distribution of points within this range.
Conversely, for the normal distribution, the sample mean is the UMVU estimator of the mean. Thus for platykurtic distributions, which can often be thought of as between a uniform distribution and a normal distribution, the informativeness of the middle sample points versus the extrema values varies from "equal" for normal to "uninformative" for uniform, and for different distributions, one or the other (or some combination thereof) may be most efficient.
A limited amount of experimental work on the efficiency of measures of central tendency for small samples by William D. Vinson reveals the following facts, where γ2 is the coefficient of excess kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
, defined as γ2 = (μ4/(μ2)²) − 3.
| Kurtosis (γ2) | Most efficient estimator of μ |
|---|---|
| -1.2 to -0.8 | Midrange |
| -0.8 to 2.0 | Arithmetic mean |
| 2.0 to 6.0 | Modified mean |
This generalization holds for sample sizes (n) from 4 to 20.
When n = 3, there can be no modified mean, and the mean is the most efficient measure of central tendency for values of γ2 form 2.0 to 6.0 as well as from −0.8 to 2.0.
Sampling properties
For a sample of size n from the standard normal distribution, the mid-range M is unbiased, and has a variance given by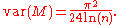For a sample of size n from the standard Laplace distribution, the mid-range M is unbiased, and has a variance given by
and, in particular, the variance does not decrease to zero as the sample size grows.
For a sample of size n from a zero-centred uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
, the mid-range M is unbiased, nM has an asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
which is a Laplace distribution.
Deviation
While the mean of a set of values minimizes the sum of squares of deviationsDeviation (statistics)
In mathematics and statistics, deviation is a measure of difference for interval and ratio variables between the observed value and the mean. The sign of deviation , reports the direction of that difference...
and the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
minimizes the average absolute deviation, the midrange minimizes the maximum deviation (defined as
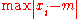): it is a solution to a variational problem.