
Interquartile mean
Encyclopedia
The interquartile mean is a statistical
measure of central tendency, much like the mean
(in more popular terms called the average
), the median
, and the mode
.
The IQM is a truncated mean
and so is very similar to the scoring method used in sports that are evaluated by a panel of judges: discard the lowest and the highest scores; calculate the mean value of the remaining scores.
is used, and the lowest 25% and the highest 25% of the scores are discarded. These points are called the first and third quartile
s, hence the name of the IQM. (Note that the second quartile is also called the median
).
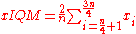
assuming the values have been ordered.
First sort the list from lowest-to-highest:
There are 12 observations (datapoints) in the dataset, thus we have 4 quartiles of 3 numbers. Discard the lowest and the highest 3 values:
We now have 6 of the 12 observations remaining; next, we calculate the arithmetic mean
of these numbers:
for symmetric distributions, e.g.:
has a mean value xmean = 3, and since it is a symmetric distribution, xIQM = 3 would be desired.
We can solve this by using a weighted average of the quartiles and the interquartile dataset:
Consider the following dataset of 9 observations:
There are 9/4 = 2.25 observations in each quartile, and 4.5 observations in the interquartile range. Truncate the fractional quartile size, and remove this number from the 1st and 3rd quartiles (2.25 observations in each quartile, thus the lowest 2 and the highest 2 are removed).
Thus, there are 3 full observations in the interquartile range, and 2 fractional observations. Since we have a total of 4.5 observations in the interquartile range, the two fractional observations each count for 0.75 (and thus 3×1 + 2×0.75 = 4.5 observations).
The IQM is now calculated as follows:
In the above example, the mean has a value xmean = 9. The same as the IQM, as was expected. The method of calculating the IQM for any number of observations is analogous; the fractional contributions to the IQM can be either 0, 0.25, 0.50, or 0.75.
as well as the median
:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
measure of central tendency, much like the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
(in more popular terms called the average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
), the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
, and the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
.
The IQM is a truncated mean
Truncated mean
A truncated mean or trimmed mean is a statistical measure of central tendency, much like the mean and median. It involves the calculation of the mean after discarding given parts of a probability distribution or sample at the high and low end, and typically discarding an equal amount of both.For...
and so is very similar to the scoring method used in sports that are evaluated by a panel of judges: discard the lowest and the highest scores; calculate the mean value of the remaining scores.
Calculation
In calculation of the IQM, only the interquartile rangeInterquartile range
In descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
is used, and the lowest 25% and the highest 25% of the scores are discarded. These points are called the first and third quartile
Quartile
In descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled...
s, hence the name of the IQM. (Note that the second quartile is also called the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
).
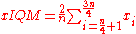
assuming the values have been ordered.
Dataset divisible by four
The method is best explained with an example. Consider the following dataset:- 5, 8, 4, 38, 8, 6, 9, 7, 7, 3, 1, 6
First sort the list from lowest-to-highest:
- 1, 3, 4, 5, 6, 6, 7, 7, 8, 8, 9, 38
There are 12 observations (datapoints) in the dataset, thus we have 4 quartiles of 3 numbers. Discard the lowest and the highest 3 values:
1, 3, 4, 5, 6, 6, 7, 7, 8,8, 9, 38
We now have 6 of the 12 observations remaining; next, we calculate the arithmetic mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of these numbers:
- xIQM = (5 + 6 + 6 + 7 + 7 + 8) / 6 = 6.5
Dataset not divisible by four
The above example consisted of 12 observations in the dataset, which made the determination of the quartiles very easy. Of course, not all datasets have a number of observations that is divisible by 4. We can adjust the method of calculating the IQM to accommodate this. Ideally we want to have the IQM equal to the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
for symmetric distributions, e.g.:
- 1, 2, 3, 4, 5
has a mean value xmean = 3, and since it is a symmetric distribution, xIQM = 3 would be desired.
We can solve this by using a weighted average of the quartiles and the interquartile dataset:
Consider the following dataset of 9 observations:
- 1, 3, 5, 7, 9, 11, 13, 15, 17
There are 9/4 = 2.25 observations in each quartile, and 4.5 observations in the interquartile range. Truncate the fractional quartile size, and remove this number from the 1st and 3rd quartiles (2.25 observations in each quartile, thus the lowest 2 and the highest 2 are removed).
1, 3, (5), 7, 9, 11, (13),15, 17
Thus, there are 3 full observations in the interquartile range, and 2 fractional observations. Since we have a total of 4.5 observations in the interquartile range, the two fractional observations each count for 0.75 (and thus 3×1 + 2×0.75 = 4.5 observations).
The IQM is now calculated as follows:
- xIQM = {(7 + 9 + 11) + 0.75 × (5 + 13)} / 4.5 = 9
In the above example, the mean has a value xmean = 9. The same as the IQM, as was expected. The method of calculating the IQM for any number of observations is analogous; the fractional contributions to the IQM can be either 0, 0.25, 0.50, or 0.75.
Comparison with mean and median
The Interquartile Mean shares some properties from both the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
as well as the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
:
- Like the medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
, the IQM is insensitive to outlierOutlierIn statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s; in the example given, the highest value (38) was an obvious outlier of the dataset, but its value is not used in the calculation of the IQM. On the other hand, the common average (the arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
) is sensitive to these outliers: xmean = 8.5. - Like the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, the IQM is a discrete parameter, based on a large number of observations from the dataset. The medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
is always equal to one of the observations in the dataset (assuming an odd number of observations). The mean can be equal to any value between the lowest and highest observation, depending on the value of all the other observations. The IQM can be equal to any value between the first and third quartiles, depending on all the observations in the interquartile range.
Applications
- London Interbank Offered RateLondon Interbank Offered RateThe LIBOR rate is the average interest rate that leading banks in London charge when lending to other banks. It is an acronym for London Interbank Offered Rate Banks borrow money for one day, one month, two months, six months, one year etc. and they pay interest to their lenders based on...
estimates a reference interest rate as the interquartile mean of the rates that several banks offer. - Everything2Everything2Everything2, Everything2, or E2 for short is a collaborative Web-based community consisting of a database of interlinked user-submitted written material. E2 is moderated for quality, but has no formal policy on subject matter...
uses the interquartile mean of the reputations of a user's writeups to determine the quality of the user's contribution.http://everything2.com/user/Professor%20Pi/writeups/Honor+Roll

