
Arago spot
Encyclopedia
In optics
, an Arago spot, Fresnel bright spot, or Poisson spot is a bright point that appears at the center of a circular object's shadow
due to Fresnel diffraction
. This spot played an important role in the discovery of the wave nature of light
(see history section below) and is a common way to demonstrate that light behaves as a wave for example in undergraduate physics laboratory exercises. The basic experimental setup is shown in the figure on the right. The wave source must be at least smaller in diameter than the circular object casting the shadow and the dimensions of the setup must comply with the requirements for Fresnel diffraction
. Namely, the Fresnel number
must satisfy
where
Finally, the edge of the circular object must be sufficiently smooth. These conditions together explain why the bright spot is not encountered in everyday life. However, with the abundance of laser sources
available today it is easy to perform a Arago spot experiment (see for example here). In astronomy
, the Arago spot can be also easily observed in the strongly defocussed image of a star
in a Newtonian telescope
. There the star provides an almost ideal point source
at infinity and the secondary mirror
of the telescope constitutes the circular obstacle.
The presence of the Arago spot can be easily understood. When light shines on a circular obstacle, Huygens' principle says that every point in the plane of the obstacle acts as a new point source of light. The light coming from points on the circumference
of the obstacle, and going to the center of the shadow, travels exactly the same distance; so all the light passing close by the object arrives at the screen in phase
and constructively interferes. This results in a bright spot at the shadow's center, where geometrical optics
and particle theories of light predict that there should be no light at all.
. It only turned out much later (in one of Einstein's Annus Mirabilis papers
) that light can be equally described as a particle (wave-particle duality of light).
At the beginning of the 19th century it became more and more evident that light does not simply propagate along straight lines (Thomas Young
published his double-slit experiment in 1807 ).
However, many still favored Isaac Newton's corpuscular theory of light, among them the great theoretician Siméon-Denis Poisson. In 1818 the French Academy launched therefore a competition to explain the properties of light, where Poisson was one of the members of the judging committee. The civil engineer Augustin-Jean Fresnel
entered this competition by submitting a new wave theory of light. Poisson studied Fresnel's theory in detail and of course looked for a way to prove it wrong being a supporter of the particle-theory of light. Poisson thought that he had found a flaw when he argued that a consequence of Fresnel’s theory was that there would exist an on-axis bright spot in the shadow of a circular obstacle, where there should be complete darkness according to the particle-theory of light. As mentioned before the Arago spot is not easily observed in every-day situations, so it was only natural for Poisson to interpret it as an absurd result and that it should disprove Fresnel's theory.
However, the head of the committee, Dominique-François-Jean Arago
, and who incidentally later became Prime Minister of France, decided to perform the experiment in more detail. He molded a 2-mm metallic disk to a glass plate with wax. To everyone's surprise he succeeded in observing the predicted spot, which convinced most scientists of the wave-nature of light. In the end Fresnel won the competition, much to Poisson's chagrin.
Arago later noted that the phenomenon (which was later to be
known as Poisson’s Spot or the Spot of Arago) had already
been observed by Delisle and Maraldi a century earlier.
, which states that every unobstructed point of a wavefront becomes the source of a secondary spherical wavelet
and that the amplitude of the optical field E at a point on the screen is given by the superposition of all those secondary wavelets taking into account their relative phases. This means that the field at a point P1 on the screen is given by a surface integral:
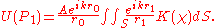
where the inclination factor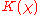 which ensures that the secondary wavelets do not propagate backwards is given by
which ensures that the secondary wavelets do not propagate backwards is given by

and
The first term outside of the integral represents the oscillations from the source wave at a distance r0. Similarly, the term inside the integral represents the oscillations from the secondary wavelets at distances r1.
In order to derive the intensity behind the circular obstacle using this integral one assumes that the experimental parameters fulfill the requirements of the near-field diffraction
regime (the size of the circular obstacle is large compared to the wavelength and small compared to the distances g=P0C and b=CP1). Going to polar coordinates then yields the integral for a circular object of radius a (see for example Born and Wolf):

This integral can be solved numerically (see below). If g is large and b is small so that the angle is not negligible one can write the integral for the on-axis case (P1 is at the center of the shadow) as (see ):
is not negligible one can write the integral for the on-axis case (P1 is at the center of the shadow) as (see ):

The source intensity
, which is the square of the field amplitude, is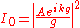 and the intensity at the screen
and the intensity at the screen  . The on-axis intensity as a function of the distance b is hence given by:
. The on-axis intensity as a function of the distance b is hence given by:
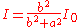
This shows that the on-axis intensity at the center of the shadow tends to the source intensity, as if the circular object was not present at all. Furthermore, this means that the Arago spot is present even just a few obstacle diameters behind the disc.
 which is 1 for transparent parts of the object plane and 0 otherwise (i.e. It is 0 if the direct line between source and the point on the screen passes through the blocking circular object.) the integral that needs to be solved is given by:
which is 1 for transparent parts of the object plane and 0 otherwise (i.e. It is 0 if the direct line between source and the point on the screen passes through the blocking circular object.) the integral that needs to be solved is given by:

Numerical calculation of the integral using the trapezoidal rule or Simpson's rule
is not efficient and becomes numerically unstable especially for configurations with large Fresnel number
. However, it is possible to solve the radial part of the integral so that only the integration over the azimuth angle remains to be done numerically. For a particular angle one must solve the line integral for the ray with origin at the intersection point of the line P0P1 with the circular object plane. The contribution for a particular ray with azimuth angle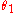 and passing a transparent part of the object plane from
and passing a transparent part of the object plane from  to
to  is:
is:

So for each angle one has to compute the intersection point(s) of the ray with the circular object and then sum the contributions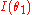 for a certain number of angles between 0 and
for a certain number of angles between 0 and  . Results of such a calculation are shown in the following images.
. Results of such a calculation are shown in the following images.
The images show simulated Arago spots in the shadow of a disc of varying diameter (4 mm, 2 mm, 1 mm – left to right) at a distance of 1 m from the disc. The point source has a wavelength of 633 nm (e.g. He-Ne Laser) and is located 1 m from the disc. The image width corresponds to 16 mm.
the intensity of the Arago spot equals that of the undisturbed wave front. Only the width of the Arago spot intensity peak depends on the distances between source, circular object and screen, as well as the source's wavelength and the diameter of the circular object. This is clear from the simulation images above. This means that one can compensate for a reduction in the source's wavelength
by increasing the distance l between circular object and screen or reducing the circular object's diameter.
The lateral intensity distribution on the screen has in fact the shape of a squared zeroth Bessel function of the first kind
when close to the optical axis
and using a plane wave source
(point source at infinity):
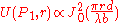
where
The following images show the radial intensity distribution of the simulated Arago spot images above:
The red lines in these three graphs correspond to the simulated images above, and the green lines were computed by applying the corresponding parameters to the squared Bessel function given above.
. Note that this is only the case if the source is close to an ideal point source. From an extended source the Arago spot is only affected marginally, since one can interpret the Arago spot as a point-spread function. And so the image of the extended source only becomes washed out due to the convolution with the point-spread function, but it does not decrease in over all intensity.
The simulation includes a regular sinusoidal corrugation of the circular shape of amplitude 10 µm, 50 µm and 100 µm, respectively. Note, that the 100 µm edge corrugation almost completely removes the central bright spot.
This effect can be best understood using the Fresnel zone concept
. The circular object blocks a certain number of Fresnel zones. The Fresnel zone that begins with the edge of the circular object is the only one that contributes to the Arago spot. All the Fresnel zones that are further out destructively interfere with each other and thus cancel. Random edge corrugation whose amplitude is of the same order as the width of that adjacent Fresnel zone reduces the Arago spot intensity. Contributions from the parts of the edge whose radius has been increased by the corrugation to about the width of the adjacent Fresnel zone now destructively interfere with those contributions from the parts which have not been affected by the corrugation.
The adjacent Fresnel zone is approximately given by:
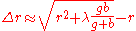
The edge corrugation should not be much more than 10% of this width to see a close to ideal Arago spot. In the above simulations with the 4 mm diameter disc the adjacent Fresnel zone has a width of about 77 µm.
molecules, so-called neutral matter waves. Material particles behave like waves as is known from quantum mechanics
. The wave-nature of particles actually dates back to de Broglie's hypothesis as well as Davisson and Germer's experiments. A Arago spot of electrons, which also constitute matter waves, can be observed in transmission electron microscopes when examining circular structures of a certain size.
The observation of an Arago spot with large molecules, and thus proving their wave-nature is a topic of current research.
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, an Arago spot, Fresnel bright spot, or Poisson spot is a bright point that appears at the center of a circular object's shadow
Shadow
A shadow is an area where direct light from a light source cannot reach due to obstruction by an object. It occupies all of the space behind an opaque object with light in front of it. The cross section of a shadow is a two-dimensional silhouette, or reverse projection of the object blocking the...
due to Fresnel diffraction
Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
. This spot played an important role in the discovery of the wave nature of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
(see history section below) and is a common way to demonstrate that light behaves as a wave for example in undergraduate physics laboratory exercises. The basic experimental setup is shown in the figure on the right. The wave source must be at least smaller in diameter than the circular object casting the shadow and the dimensions of the setup must comply with the requirements for Fresnel diffraction
Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
. Namely, the Fresnel number
Fresnel number
The Fresnel number F, named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory....
must satisfy
where
- d is the diameter of the circular object
- l is the distance between the object and the screen
- λ the wavelength of the source
Finally, the edge of the circular object must be sufficiently smooth. These conditions together explain why the bright spot is not encountered in everyday life. However, with the abundance of laser sources
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
available today it is easy to perform a Arago spot experiment (see for example here). In astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, the Arago spot can be also easily observed in the strongly defocussed image of a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
in a Newtonian telescope
Newtonian telescope
The Newtonian telescope is a type of reflecting telescope invented by the British scientist Sir Isaac Newton , using a concave primary mirror and a flat diagonal secondary mirror. Newton’s first reflecting telescope was completed in 1668 and is the earliest known functional reflecting telescope...
. There the star provides an almost ideal point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
at infinity and the secondary mirror
Secondary mirror
A secondary mirror is the second deflecting or focusing mirror element in a reflecting telescope. Light gathered by the primary mirror is directed towards a focal point typically past the location of the secondary. Secondary mirrors in the form of an optically flat diagonal mirror are used to...
of the telescope constitutes the circular obstacle.
The presence of the Arago spot can be easily understood. When light shines on a circular obstacle, Huygens' principle says that every point in the plane of the obstacle acts as a new point source of light. The light coming from points on the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of the obstacle, and going to the center of the shadow, travels exactly the same distance; so all the light passing close by the object arrives at the screen in phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
and constructively interferes. This results in a bright spot at the shadow's center, where geometrical optics
Geometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
and particle theories of light predict that there should be no light at all.
History
The original Arago spot experiment was carried out in the beginning of the 19th century and played an important role in the history of science. Then it turned out to be the deciding experiment of whether light is a particle or a wave. It is thus a great example of a so-called experimentum crucisExperimentum crucis
In the sciences, an experimentum crucis is an experiment capable of decisively determining whether or not a particular hypothesis or theory is superior to all other hypotheses or theories whose acceptance is currently widespread in the scientific community...
. It only turned out much later (in one of Einstein's Annus Mirabilis papers
Annus Mirabilis Papers
The Annus Mirabilis papers are the papers of Albert Einstein published in the Annalen der Physik scientific journal in 1905. These four articles contributed substantially to the foundation of modern physics and changed views on space, time, and matter...
) that light can be equally described as a particle (wave-particle duality of light).
At the beginning of the 19th century it became more and more evident that light does not simply propagate along straight lines (Thomas Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
published his double-slit experiment in 1807 ).
However, many still favored Isaac Newton's corpuscular theory of light, among them the great theoretician Siméon-Denis Poisson. In 1818 the French Academy launched therefore a competition to explain the properties of light, where Poisson was one of the members of the judging committee. The civil engineer Augustin-Jean Fresnel
Augustin-Jean Fresnel
Augustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....
entered this competition by submitting a new wave theory of light. Poisson studied Fresnel's theory in detail and of course looked for a way to prove it wrong being a supporter of the particle-theory of light. Poisson thought that he had found a flaw when he argued that a consequence of Fresnel’s theory was that there would exist an on-axis bright spot in the shadow of a circular obstacle, where there should be complete darkness according to the particle-theory of light. As mentioned before the Arago spot is not easily observed in every-day situations, so it was only natural for Poisson to interpret it as an absurd result and that it should disprove Fresnel's theory.
However, the head of the committee, Dominique-François-Jean Arago
François Arago
François Jean Dominique Arago , known simply as François Arago , was a French mathematician, physicist, astronomer and politician.-Early life and work:...
, and who incidentally later became Prime Minister of France, decided to perform the experiment in more detail. He molded a 2-mm metallic disk to a glass plate with wax. To everyone's surprise he succeeded in observing the predicted spot, which convinced most scientists of the wave-nature of light. In the end Fresnel won the competition, much to Poisson's chagrin.
Arago later noted that the phenomenon (which was later to be
known as Poisson’s Spot or the Spot of Arago) had already
been observed by Delisle and Maraldi a century earlier.
Theory
At the heart of Fresnel's wave theory is the Huygens-Fresnel principleHuygens-Fresnel principle
The Huygens–Fresnel principle is a method of analysis applied to problems of wave propagation both in the far-field limit and in near-field diffraction.-History:...
, which states that every unobstructed point of a wavefront becomes the source of a secondary spherical wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
and that the amplitude of the optical field E at a point on the screen is given by the superposition of all those secondary wavelets taking into account their relative phases. This means that the field at a point P1 on the screen is given by a surface integral:
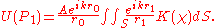
where the inclination factor
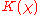 which ensures that the secondary wavelets do not propagate backwards is given by
which ensures that the secondary wavelets do not propagate backwards is given by
and
- A is the amplitude of the source wave
-
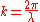 is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector... - S is the unobstructed surface
The first term outside of the integral represents the oscillations from the source wave at a distance r0. Similarly, the term inside the integral represents the oscillations from the secondary wavelets at distances r1.
In order to derive the intensity behind the circular obstacle using this integral one assumes that the experimental parameters fulfill the requirements of the near-field diffraction
Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
regime (the size of the circular obstacle is large compared to the wavelength and small compared to the distances g=P0C and b=CP1). Going to polar coordinates then yields the integral for a circular object of radius a (see for example Born and Wolf):

This integral can be solved numerically (see below). If g is large and b is small so that the angle
 is not negligible one can write the integral for the on-axis case (P1 is at the center of the shadow) as (see ):
is not negligible one can write the integral for the on-axis case (P1 is at the center of the shadow) as (see ):
The source intensity
Intensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
, which is the square of the field amplitude, is
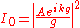 and the intensity at the screen
and the intensity at the screen  . The on-axis intensity as a function of the distance b is hence given by:
. The on-axis intensity as a function of the distance b is hence given by: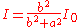
This shows that the on-axis intensity at the center of the shadow tends to the source intensity, as if the circular object was not present at all. Furthermore, this means that the Arago spot is present even just a few obstacle diameters behind the disc.
Calculation of diffraction images
To calculate the full diffraction image that is visible on the screen one has to consider the surface integral of the previous section. One cannot exploit circular symmetry anymore, since the line between the source and an arbitrary point on the screen does not pass through the center of the circular object. With the aperture function which is 1 for transparent parts of the object plane and 0 otherwise (i.e. It is 0 if the direct line between source and the point on the screen passes through the blocking circular object.) the integral that needs to be solved is given by:
which is 1 for transparent parts of the object plane and 0 otherwise (i.e. It is 0 if the direct line between source and the point on the screen passes through the blocking circular object.) the integral that needs to be solved is given by:
Numerical calculation of the integral using the trapezoidal rule or Simpson's rule
Simpson's rule
In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...
is not efficient and becomes numerically unstable especially for configurations with large Fresnel number
Fresnel number
The Fresnel number F, named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory....
. However, it is possible to solve the radial part of the integral so that only the integration over the azimuth angle remains to be done numerically. For a particular angle one must solve the line integral for the ray with origin at the intersection point of the line P0P1 with the circular object plane. The contribution for a particular ray with azimuth angle
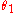 and passing a transparent part of the object plane from
and passing a transparent part of the object plane from  to
to  is:
is:
So for each angle one has to compute the intersection point(s) of the ray with the circular object and then sum the contributions
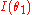 for a certain number of angles between 0 and
for a certain number of angles between 0 and  . Results of such a calculation are shown in the following images.
. Results of such a calculation are shown in the following images.The images show simulated Arago spots in the shadow of a disc of varying diameter (4 mm, 2 mm, 1 mm – left to right) at a distance of 1 m from the disc. The point source has a wavelength of 633 nm (e.g. He-Ne Laser) and is located 1 m from the disc. The image width corresponds to 16 mm.
Experimental aspects
Observation of the Arago spot with a conventional light source can be challenging. This section summarizes how the various experimental parameters affect the visibility of the Arago spot.Intensity and size
For an ideal point sourcePoint source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
the intensity of the Arago spot equals that of the undisturbed wave front. Only the width of the Arago spot intensity peak depends on the distances between source, circular object and screen, as well as the source's wavelength and the diameter of the circular object. This is clear from the simulation images above. This means that one can compensate for a reduction in the source's wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
by increasing the distance l between circular object and screen or reducing the circular object's diameter.
The lateral intensity distribution on the screen has in fact the shape of a squared zeroth Bessel function of the first kind
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
when close to the optical axis
Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
and using a plane wave source
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
(point source at infinity):
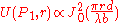
where
- r is the distance of the point
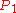 on the screen from the optical axis
on the screen from the optical axis - d is the diameter of circular object
-
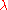 is the wavelength
is the wavelength - b is the distance between circular object and screen
The following images show the radial intensity distribution of the simulated Arago spot images above:
The red lines in these three graphs correspond to the simulated images above, and the green lines were computed by applying the corresponding parameters to the squared Bessel function given above.
Finite source size and spatial coherence
The main reason why the Arago spot is hard to observe in circular shadows from conventional light sources is that such light sources are bad approximations of point sources. If the wave source has a finite size S then the Arago spot will have an extent that is given by S×b/g, as if the circular object acted like a lens. At the same time the intensity of the Arago spot is reduced with respect to the intensity of the undisturbed wave front.Deviation from circularity
If the cross-section of the circular object deviates slightly from its circular shape (but it still has a sharp edge on a smaller scale) the shape of the point-source Arago spot changes. In particular, if the object has an ellipsoidal cross-section the Arago spot has the shape of an evoluteEvolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
. Note that this is only the case if the source is close to an ideal point source. From an extended source the Arago spot is only affected marginally, since one can interpret the Arago spot as a point-spread function. And so the image of the extended source only becomes washed out due to the convolution with the point-spread function, but it does not decrease in over all intensity.
The circular object's surface roughness
The Arago spot is very sensitive to small-scale deviations from the ideal circular cross-section. This means that a small amount of surface roughness of the circular object can completely cancel out the bright spot. This is shown in the following three diagrams which are simulations of the Arago spot from a 4 mm diameter disc (g = b = 1 m):The simulation includes a regular sinusoidal corrugation of the circular shape of amplitude 10 µm, 50 µm and 100 µm, respectively. Note, that the 100 µm edge corrugation almost completely removes the central bright spot.
This effect can be best understood using the Fresnel zone concept
Fresnel zone
In optics and radio communications , a Fresnel zone , named for physicist Augustin-Jean Fresnel, is one of a number of concentric ellipsoids which define volumes in the radiation pattern of a circular aperture...
. The circular object blocks a certain number of Fresnel zones. The Fresnel zone that begins with the edge of the circular object is the only one that contributes to the Arago spot. All the Fresnel zones that are further out destructively interfere with each other and thus cancel. Random edge corrugation whose amplitude is of the same order as the width of that adjacent Fresnel zone reduces the Arago spot intensity. Contributions from the parts of the edge whose radius has been increased by the corrugation to about the width of the adjacent Fresnel zone now destructively interfere with those contributions from the parts which have not been affected by the corrugation.
The adjacent Fresnel zone is approximately given by:
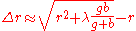
The edge corrugation should not be much more than 10% of this width to see a close to ideal Arago spot. In the above simulations with the 4 mm diameter disc the adjacent Fresnel zone has a width of about 77 µm.
Arago spot with matter waves
Recently, the Arago spot experiment has been demonstrated with a supersonic expansion beam of deuteriumDeuterium
Deuterium, also called heavy hydrogen, is one of two stable isotopes of hydrogen. It has a natural abundance in Earth's oceans of about one atom in of hydrogen . Deuterium accounts for approximately 0.0156% of all naturally occurring hydrogen in Earth's oceans, while the most common isotope ...
molecules, so-called neutral matter waves. Material particles behave like waves as is known from quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The wave-nature of particles actually dates back to de Broglie's hypothesis as well as Davisson and Germer's experiments. A Arago spot of electrons, which also constitute matter waves, can be observed in transmission electron microscopes when examining circular structures of a certain size.
The observation of an Arago spot with large molecules, and thus proving their wave-nature is a topic of current research.


