Analytic signal
Encyclopedia
In mathematics
and signal processing
, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency
components of the Fourier transform
(or spectrum
) of a real-valued
function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, providing one is willing to deal with a complex-valued function instead. That makes certain attributes of the signal more accessible and facilitate the derivation of modulation and demodulation techniques, especially single-sideband. As long as the manipulated function has no negative frequency components (that is, it is still analytic), the conversion from complex back to real is just a matter of discarding the imaginary part. The analytic representation is a generalization of the phasor concept: while the phasor is restricted to time-invariant amplitude, phase, and frequency, the analytic signal allows for time-variable parameters.
, then the function: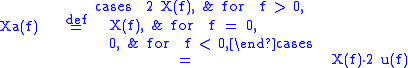
contains only the non-negative frequency components of X(f). And the operation is reversible, due to the Hermitian property of X(f):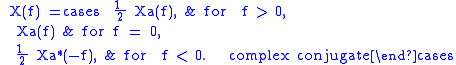
The inverse Fourier transform of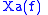
is the analytic signal:
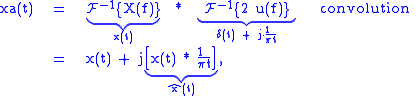
where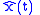
is the Hilbert transform
of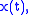
and 
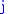is the imaginary unit
.
It also follows from Euler's formula
that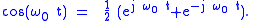
So 
comprises both positive and negative frequency
components.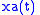
is just the positive portion. When dealing with simple sinusoids or sums of sinusoids, we can deduce 
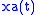directly, without determining 
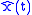first.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency
Negative frequency
The concept of negative and positive frequency can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation...
components of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
(or spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
) of a real-valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, providing one is willing to deal with a complex-valued function instead. That makes certain attributes of the signal more accessible and facilitate the derivation of modulation and demodulation techniques, especially single-sideband. As long as the manipulated function has no negative frequency components (that is, it is still analytic), the conversion from complex back to real is just a matter of discarding the imaginary part. The analytic representation is a generalization of the phasor concept: while the phasor is restricted to time-invariant amplitude, phase, and frequency, the analytic signal allows for time-variable parameters.
Definition
If x(t) is a real-valued signal with Fourier transform X(f), and u(f) is the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
, then the function:
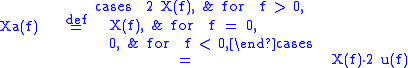
contains only the non-negative frequency components of X(f). And the operation is reversible, due to the Hermitian property of X(f):
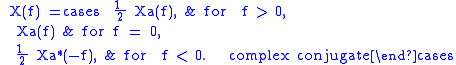
The inverse Fourier transform of
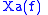is the analytic signal: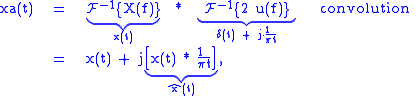where
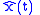is the Hilbert transformHilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
of
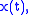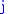and is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
- Example 1:
, for some real parameter 
-
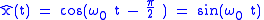
(The 2nd equality is Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
.)- This is a complex-valued signal with increasing phase (positive frequency).
It also follows from Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
that
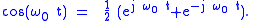So comprises both positive and negative frequencyNegative frequency
The concept of negative and positive frequency can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation...
components.
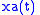is just the positive portion. When dealing with simple sinusoids or sums of sinusoids, we can deduce 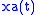directly, without determining 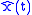first.- Example 2:
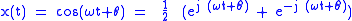
The removal of the negative frequency terms is also demonstrated in Example 3. We note that nothing prevents us from computing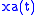
for a complex-valued 
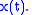But it might not be a reversible representation, because the original spectrum is not symmetrical in general. So except for this example, the general discussion assumes real-valued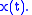 
- Example 3:
, for some real parameter 
Analytic signals are often shifted in frequency (down-converted) toward 0 Hz, which creates [non-symmetrical] negative frequency components. One motive is to allow lowpass filters with real coefficients to be used to limit the bandwidth of the signal. Another motive is to reduce the highest frequency, which reduces the minimum rate for alias-free sampling. A frequency shift does not undermine the mathematical tractability of the complex signal representation. So in that sense, the down-converted signal is still "analytic". However, restoring the real-valued representation is no longer a simple matter of just extracting the real component. Up-conversion is obviously required, and if the signal has been sampledSampling (signal processing)In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
(discrete-time), interpolationInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
(upsamplingUpsamplingUpsampling is the process of increasing the sampling rate of a signal. For instance, upsampling raster images such as photographs means increasing the resolution of the image....
) might also be necessary to avoid aliasingAliasingIn signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
.
The complex conjugate of an analytic signal contains only negative frequency components. In that case also, there is no loss of information or reversibility by discarding the imaginary component. Obviously the real component of the complex conjugate is the same as the real component of the analytic signal. But in this case, its extraction restores the suppressed positive frequency components.
Another way to achieve a spectrum of negative frequencies is to frequency-shift the analytic signal sufficiently far in the negative direction. Extracting the real component again restores the positive frequencies. But in this case their order is reversed... the low-frequency component is now the high one. This can be used to demodulate a type of single sideband signal called lower sideband or inverted sideband.
Applications
The analytic signal can also be expressed in terms of complex polar coordinates,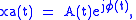
where:
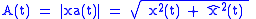
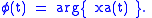(see arg functionArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
)
These functions are respectively called the amplitude envelopeEnvelope detectorAn envelope detector is an electronic circuit that takes a high-frequency signal as input and provides an output which is the "envelope" of the original signal. The capacitor in the circuit stores up charge on the rising edge, and releases it slowly through the resistor when the signal falls...
and instantaneous phaseInstantaneous phaseThe notions of Instantaneous Phase and Instantaneous Frequency are important concepts in Signal Processing that occur in the context of the representation and analysis of time-varying signals....
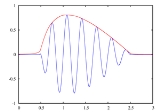
of the signal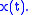
In the accompanying diagram, the blue curve depicts 
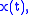and the red curve depicts the corresponding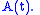 
The time derivative of the unwrapped instantaneous phase is called the instantaneous frequency:.
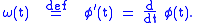
The amplitude function, and the instantaneous phase and frequency are in some applications used to measure and detect local features of the signal. Another application of the analytic representation of a signal relates to demodulation of modulated signalsModulationIn electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
. The polar coordinates conveniently separate the effects of amplitude modulationAmplitude modulationAmplitude modulation is a technique used in electronic communication, most commonly for transmitting information via a radio carrier wave. AM works by varying the strength of the transmitted signal in relation to the information being sent...
and phase (or frequency) modulation, and effectively demodulates certain kinds of signals.
The analytic signal can also be represented as: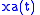
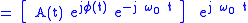
where
is the signal's complex envelope. The complex envelope is not unique; on the contrary, it is determined by an arbitrary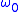
assignment. This concept is often used when dealing with passband signals. If 
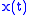is a modulated signal, 
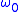is usually assigned to be a carrier frequency. In other cases it is selected to be somewhere in the middle of the frequency band. Sometimes 
is chosen to minimize
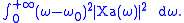
Alternatively http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1163321,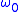
can be chosen to minimize the mean square error in linearly approximating the unwrapped instantaneous phase 
:
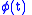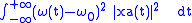
or another alternative (for some optimum
):
.
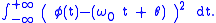In the field of time-frequency signal processing, it was shown that the analytic signal was needed in the definition of the Wigner-Ville Distribution so that the method can have the desirable properties needed for practical applications. More details and other applications can be found in.
Extensions of the analytic signal to signals of multiple variables
The concept of analytic signal is well-defined for signals of a single variable which typically is time. For signals of two or more variables, an analytic signal can be defined in different ways, and two approaches are presented below.
Multi-dimensional analytic signal based on an ad-hoc direction
A straightforward generalization of the analytic signal can be done for a multi-dimensional signal once it is established what is meant by negative frequencies for this case. This can be done by introducing a normalized vector
in the Fourier domain and label any frequency vector 
as negative if 
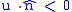. The analytic signal is then produced by removing all negative frequencies and multiply the result by 2, in accordance to the procedure described for the case of one-variable signals. However, there is no particular direction for 
which must be chosen unless there are some additional constraints. Therefore, the choice of 
is ad-hoc, or application specific.
The monogenic signal
The real and imaginary parts of the analytic signal correspond to the two elements of the vector-valued monogenic signal, as it is defined for one-variable signals. However, the monogenic signal can be extended to arbitrary number of variables in a straightforward manner, producing an (n + 1)-dimensional vector-valued function for the case of n-variable signals.
Not to be confused with
In mathematics, particularly functions of a complex variable, an analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
refers to a function which satisfies certain properties regarding differentiability. The concept of analytic signal should not be confused with analytic functions. See the analytic representation related to the Hilbert transform for a discussion about the relation between these two concepts.
See also
- Practical considerations for computing Hilbert transforms
- Negative frequencyNegative frequencyThe concept of negative and positive frequency can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation...
- Single sideband modulation (application)
- Quadrature filter (application)
- Causal filterCausal filterIn signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
(application)
External links
- Example 3:
