Negative frequency
Encyclopedia
The concept of negative and positive frequency
can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation. The rate is expressed in units such as revolutions (aka cycles) per second (hertz
) or radian/second (where 1 cycle corresponds to 2π radian
s).
) steadily increases or decreases. When the angle is a function of time, the concept of negative frequency is sometimes used to distinguish a decreasing angle from an increasing one. But sinusoids are not monotonic function
s. Consequently,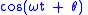
does not preserve the sign of 
, just as 
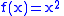does not preserve the sign of 
. Note that 
represents a usually unknown, random phase offset. In most cases of dealing with a single, real-valued sinusoid, it is sufficient to assume that 
is positive. It represents the frequency, in units of radian/s.
Sometimes there are two sinusoids with the same frequency, and a known phase difference, for instance: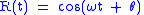
and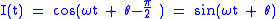
When
, 
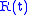appears to lead 
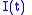by 
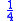cycle (
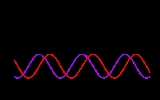
radians). But when 
, the roles are reversed. So in that case it is possible to distinguish negative and positive frequencies. The diagram depicts a negative frequency. 
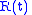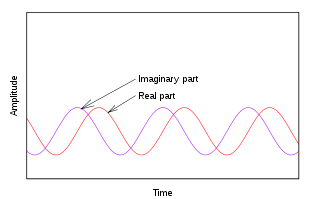
and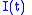 
are referred to as real and imaginary, respectively. And 
.
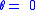A parametric plot of imaginary vs real would trace a circular path (like the rotating wheel). The addition of a time dimension creates a corkscrew pattern. A negative frequency (decreasing phase) causes a clockwise rotation in a right hand coordinate system as time increases:
facilitates many kinds of mathematical operations involving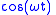 
, due in large part to Euler's simplification
:
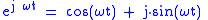
This very useful form is often referred to as a complex sinusoid, and it preserves the distinction between positive and negative
.
The Fourier transform
of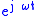
produces a non-zero response only at frequency 
.
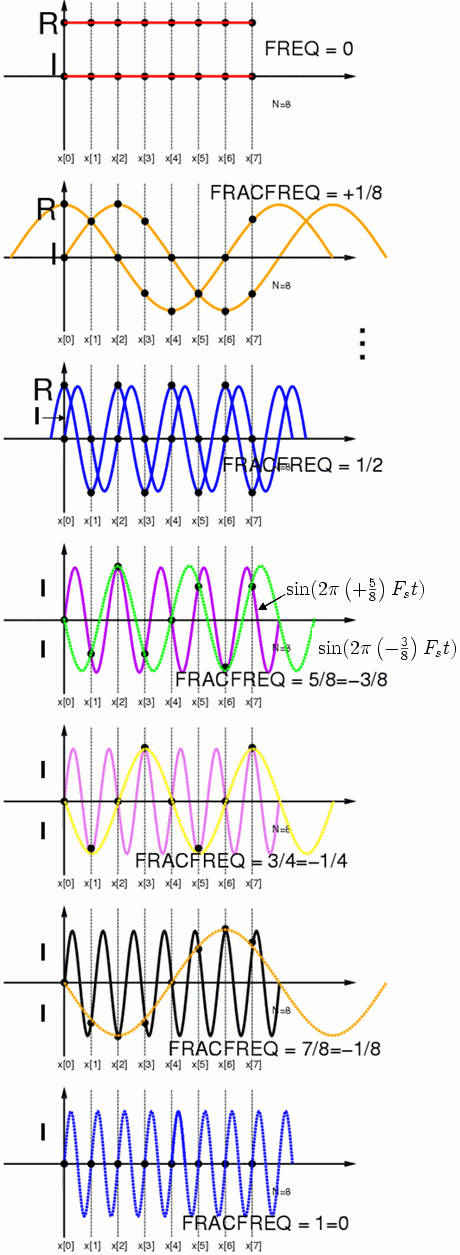
When a complex sinusoid is sampled at regular intervals, its frequency becomes indistinguishable from certain other frequencies, including negative ones (referred to as aliasing
). The adjacent figure illustrates this effect for several cases. The red indicates 0 Hz (aka DC). Successively higher frequencies are indicated by orange, blue, purple, violet, black, and blue. Note that some frames depict "R" and "I" for the same frequency, and others depict the "I" samples of different frequencies that are aliases of each other.
For instance, the fourth frame (purple and green) compares samples of the imaginary component of the fractional frequency +
with those of negative frequency 
, to illustrate that they are indistinguishable. Or in other words: 
for integer values of n, representing the sample number. The underlying waveforms are just the imaginary components of: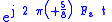 
and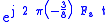 
, where 
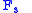is the sample rate (samples/sec).
Likewise +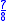
is indistinguishable from 
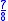. And 
(last plot) is indistinguishable from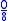 
(first plot).
begin at zero frequency, and get more negative as we move downward, row by row. This is because each of these rows functions as a matched filter
to measure increasingly positive frequencies in the signal under test. For example, the top row of the 8 point DFT matrix measures DC in the signal, while the next row, which is a signal of fractional frequency −1/8, measures the strength at +1/8 fractional frequency in the signal under test.
, the usual convention is that objects moving toward the radar are considered to induce a positive (differential) frequency, and objects going away are considered to induce a negative frequency.
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation. The rate is expressed in units such as revolutions (aka cycles) per second (hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
) or radian/second (where 1 cycle corresponds to 2π radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s).
Sinusoids
A sinusoid is a function of an angular argument, and its amplitude varies cyclically as the angle (aka phasePhase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
) steadily increases or decreases. When the angle is a function of time, the concept of negative frequency is sometimes used to distinguish a decreasing angle from an increasing one. But sinusoids are not monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
s. Consequently,
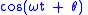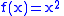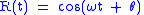
does not preserve the sign of , just as does not preserve the sign of . Note that represents a usually unknown, random phase offset. In most cases of dealing with a single, real-valued sinusoid, it is sufficient to assume that is positive. It represents the frequency, in units of radian/s.and
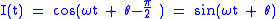
When
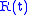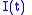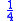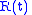, appears to lead by cycle ( radians). But when , the roles are reversed. So in that case it is possible to distinguish negative and positive frequencies. The diagram depicts a negative frequency. and 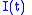are referred to as real and imaginary, respectively. And .Complex sinusoids
The complex function: facilitates many kinds of mathematical operations involving 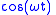, due in large part to Euler's simplificationEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
:
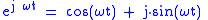
This very useful form is often referred to as a complex sinusoid, and it preserves the distinction between positive and negative
.
- For positive values, it is also called the analytic representationAnalytic signalIn mathematics and signal processing, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency components of the Fourier transform of a real-valued function are superfluous, due to the...
of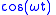
.
The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of
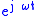produces a non-zero response only at frequency .
- The transform of
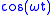has responses at both 
and 
, which reflects the fact that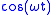 
is insufficient to determine the sign of 
.
- An alternative, and surprisingly useful, viewpoint is that both frequencies are present, as implied by the inverse of Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
:
.
- An alternative, and surprisingly useful, viewpoint is that both frequencies are present, as implied by the inverse of Euler's formula
Sampling of positive and negative frequencies and aliasing
When a complex sinusoid is sampled at regular intervals, its frequency becomes indistinguishable from certain other frequencies, including negative ones (referred to as aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
). The adjacent figure illustrates this effect for several cases. The red indicates 0 Hz (aka DC). Successively higher frequencies are indicated by orange, blue, purple, violet, black, and blue. Note that some frames depict "R" and "I" for the same frequency, and others depict the "I" samples of different frequencies that are aliases of each other.
For instance, the fourth frame (purple and green) compares samples of the imaginary component of the fractional frequency +
with those of negative frequency , to illustrate that they are indistinguishable. Or in other words: for integer values of n, representing the sample number. The underlying waveforms are just the imaginary components of: 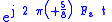and 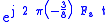, where 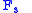is the sample rate (samples/sec).Likewise +
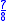is indistinguishable from 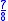. And (last plot) is indistinguishable from 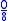(first plot).Negative frequency as a matched filter for positive frequencies
The rows of the DFT matrixDFT matrix
A DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
begin at zero frequency, and get more negative as we move downward, row by row. This is because each of these rows functions as a matched filter
Matched filter
In telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
to measure increasingly positive frequencies in the signal under test. For example, the top row of the 8 point DFT matrix measures DC in the signal, while the next row, which is a signal of fractional frequency −1/8, measures the strength at +1/8 fractional frequency in the signal under test.
Negative frequency in Doppler radar
In Doppler radarDoppler radar
A Doppler radar is a specialized radar that makes use of the Doppler effect to produce velocity data about objects at a distance. It does this by beaming a microwave signal towards a desired target and listening for its reflection, then analyzing how the frequency of the returned signal has been...
, the usual convention is that objects moving toward the radar are considered to induce a positive (differential) frequency, and objects going away are considered to induce a negative frequency.