Quadrature filter
Encyclopedia
In signal processing
, a quadrature filter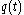
is the analytic representation
of the impulse response
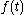of a real-valued filter:
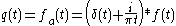
If the quadrature filter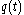
is applied to a signal 
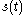, the result is
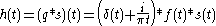
which implies that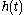
is the analytic representation of 
.
Since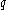
is an analytic signal, it is either zero or complex-valued. In practice, therefore, 
is often implemented as two real-valued filters, which correspond to the real and imaginary parts of the filter, respectively.
An ideal quadrature filter cannot have a finite support
, but by choosing the function
carefully, it is possible to design quadrature filters which are localized such that they can be approximated reasonably well by means of functions of finite support
.
for general signals cannot be made in practice since it involves convolutions with the function
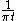
which is difficult to approximate as a filter which is either causal or of finite support
, or both. According to the above result, however, it is possible to obtain an analytic signal by convolving the signal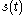
with a quadrature filter 
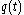. Given that 
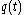is designed with some care, it can be approximated by means of a filter which can be implemented in practice. The resulting function 
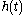is the analytic signal of 
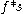rather than of 
. This implies that 
should be chosen such that convolution by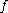 
affects the signal as little as possible. Typically, 
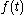is a band-pass filter, removing low and high frequencies, but allowing frequencies within a range which includes the interesting components of the signal to pass.
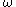the magnitude of the response of a quadrature filter equals the signal's amplitude A times the frequency function of the filter at frequency 
.
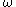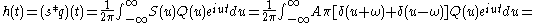
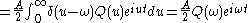
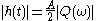
This property can be useful when the signal s is a narrow-bandwidth signal of unknown frequency. By choosing a suitable frequency function Q of the filter, we may generate known functions of the unknown frequency
which then can be estimated.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, a quadrature filter
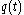is the analytic representationAnalytic signal
In mathematics and signal processing, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency components of the Fourier transform of a real-valued function are superfluous, due to the...
of the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
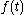of a real-valued filter: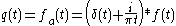If the quadrature filter
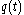is applied to a signal 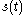, the result is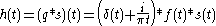which implies that
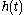is the analytic representation of .Since
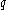is an analytic signal, it is either zero or complex-valued. In practice, therefore, is often implemented as two real-valued filters, which correspond to the real and imaginary parts of the filter, respectively.An ideal quadrature filter cannot have a finite support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
, but by choosing the function
carefully, it is possible to design quadrature filters which are localized such that they can be approximated reasonably well by means of functions of finite supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
.
Estimation of analytic signal
Notice that the computation of an ideal analytic signalAnalytic signal
In mathematics and signal processing, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency components of the Fourier transform of a real-valued function are superfluous, due to the...
for general signals cannot be made in practice since it involves convolutions with the function
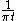
which is difficult to approximate as a filter which is either causal or of finite support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
, or both. According to the above result, however, it is possible to obtain an analytic signal by convolving the signal
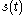with a quadrature filter 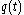. Given that 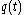is designed with some care, it can be approximated by means of a filter which can be implemented in practice. The resulting function 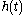is the analytic signal of 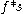rather than of . This implies that should be chosen such that convolution by 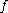affects the signal as little as possible. Typically, 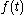is a band-pass filter, removing low and high frequencies, but allowing frequencies within a range which includes the interesting components of the signal to pass.Single frequency signals
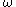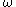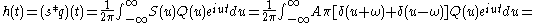
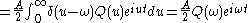
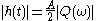
For single frequency signals (in practice narrow bandwidth signals) with frequency the magnitude of the response of a quadrature filter equals the signal's amplitude A times the frequency function of the filter at frequency .This property can be useful when the signal s is a narrow-bandwidth signal of unknown frequency. By choosing a suitable frequency function Q of the filter, we may generate known functions of the unknown frequency
which then can be estimated.