
Instantaneous phase
Encyclopedia
The notions of Instantaneous Phase and Instantaneous Frequency are important concepts in Signal Processing
that occur in the context of the representation and analysis of time-varying signals.
In signal processing
, the instantaneous phase (or "local phase" or simply "phase") of a complex-valued function is the real-valued function:
is the real-valued function: (see arg function
(see arg function
)
And for a real-valued signal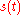 it is determined from the signal's analytic representation
it is determined from the signal's analytic representation
,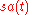 :
:

When is constrained to an interval such as
is constrained to an interval such as 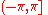 or
or 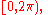 it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument
it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument  assuming
assuming  is a continuous function of
is a continuous function of  Unless otherwise indicated, the continuous form should be inferred.
Unless otherwise indicated, the continuous form should be inferred.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
that occur in the context of the representation and analysis of time-varying signals.
In signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the instantaneous phase (or "local phase" or simply "phase") of a complex-valued function
 is the real-valued function:
is the real-valued function: (see arg function
(see arg functionArg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
)
And for a real-valued signal
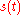 it is determined from the signal's analytic representation
it is determined from the signal's analytic representationAnalytic signal
In mathematics and signal processing, the analytic representation of a real-valued function or signal facilitates many mathematical manipulations of the signal. The basic idea is that the negative frequency components of the Fourier transform of a real-valued function are superfluous, due to the...
,
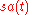 :
:
When
 is constrained to an interval such as
is constrained to an interval such as 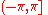 or
or 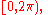 it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument
it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument  assuming
assuming  is a continuous function of
is a continuous function of  Unless otherwise indicated, the continuous form should be inferred.
Unless otherwise indicated, the continuous form should be inferred.Examples
- Example 1:
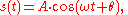 where
where 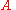 and
and  are positive values.
are positive values.
-

- Example 2:

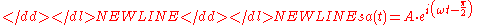
For both of these sinusoidal examples, the local maxima of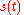 correspond to
correspond to

for integer values of . Similarly, the local minima correspond to
. Similarly, the local minima correspond to

and the maximum rates of change correspond to
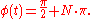
For signals that are approximately sinusoidal, these properties can be used, e.g., in image processingImage processingIn electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, to detect points that are close to edges or lines, and also to measure the position of these points with sub-pixelPixelIn digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
accuracy.
Instantaneous frequency
In general, the instantaneous angular frequency is defined as
- and the instantaneous frequency (Hz) is:
-
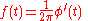 .
.
Conversely, the unwrapped phase can be represented in terms of an instantaneous frequency. When it is actually constructed/derived this way, this process is called phase unwrapping: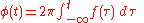

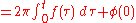
A similar definition can be used to describe phase as a function of frequency. In this case, the complex notation of phase generates values from ±180 degrees, but for unwrapped phase, an additional 360 degrees of phase must be added when the phase moves from +180 to -180 degrees. In this way, the phase will accumulate to any arbitrarily large value. Note from the definition that the phase function must exist for all frequency from f=0. In many cases, such as RF and Microwave measurements of cables or filters, the phase response is not measured continuously, but from some non-zero start frequency. In this case, phase unwrapping has ambiguities due to the lack of knowledge of phase response before the start frequency. In this case, it is common practice to assign the integral a value of zero for phase response before the start frequency. For devices such as cables, which have nearly constant phase vs frequency, this can give an error in the unwrapped phase response compared to the expected value as the phase before the start frequency is not included.
Complex representation
In some applications, such as averaging the values of phase at several moments of time, it may be useful to convert each value to a complex number, or vector representation:
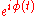
 (Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
(Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
)
This representation is similar to the wrapped phase representation in that it does not distinguish between multiples of in the phase, but similar to the unwrapped phase representation since it is continuous. A vector-average phase can be obtained as the argArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
in the phase, but similar to the unwrapped phase representation since it is continuous. A vector-average phase can be obtained as the argArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
of the sum of the complex numbers.-
-




