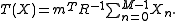Uniformly most powerful test
Encyclopedia
In statistical hypothesis testing
, a uniformly most powerful (UMP) test is a hypothesis test
which has the greatest power
1 − β among all possible tests of a given size
α. For example, according to the Neyman–Pearson lemma, the likelihood-ratio test is UMP for testing simple (point) hypotheses.
 denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density function
denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density function
s or probability mass function
s , which depends on the unknown deterministic parameter
, which depends on the unknown deterministic parameter  . The parameter space
. The parameter space  is partitioned into two disjoint sets
is partitioned into two disjoint sets 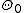 and
and 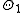 . Let
. Let  denote the hypothesis that
denote the hypothesis that  , and let
, and let 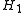 denote the hypothesis that
denote the hypothesis that 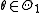 .
.
The binary test of hypotheses is performed using a test function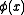 .
.
meaning that is in force if the measurement
is in force if the measurement  and that
and that  is in force if the measurement
is in force if the measurement  .
.
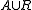 is a disjoint covering of the measurement space.
is a disjoint covering of the measurement space.
 is UMP of size
is UMP of size  if for any other test function
if for any other test function 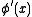 we have:
we have: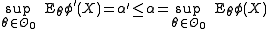
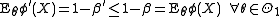
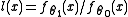 .
.
If is monotone non-decreasing, in
is monotone non-decreasing, in  , for any pair
, for any pair 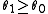 (meaning that the greater
(meaning that the greater  is, the more likely
is, the more likely  is), then the threshold test:
is), then the threshold test: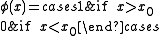

is the UMP test of size α for testing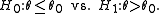
Note that exactly the same test is also UMP for testing
of probability density function
s or probability mass function
s with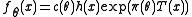
has a monotone non-decreasing likelihood ratio in the sufficient statistic
T(x), provided that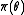 is non-decreasing.
is non-decreasing.
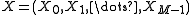 denote i.i.d. normally distributed
denote i.i.d. normally distributed 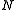 -dimensional random vectors with mean
-dimensional random vectors with mean 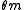 and covariance matrix
and covariance matrix 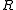 . We then have
. We then have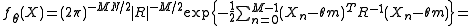

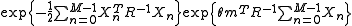
which is exactly in the form of the exponential family shown in the previous section, with the sufficient statistic being
Thus, we conclude that the test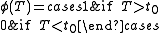
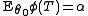
is the UMP test of size for testing
for testing 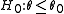 vs.
vs. 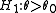
The reason is that in these situations, the most powerful test of a given size for one possible value of the parameter (e.g. for where
where 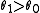 ) is different from the most powerful test of the same size for a different value of the parameter (e.g. for
) is different from the most powerful test of the same size for a different value of the parameter (e.g. for 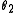 where
where 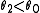 ). As a result, no test is uniformly most powerful.
). As a result, no test is uniformly most powerful.
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
, a uniformly most powerful (UMP) test is a hypothesis test
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
which has the greatest power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
1 − β among all possible tests of a given size
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
α. For example, according to the Neyman–Pearson lemma, the likelihood-ratio test is UMP for testing simple (point) hypotheses.
Setting
Let denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density function
denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s or probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
s
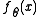 , which depends on the unknown deterministic parameter
, which depends on the unknown deterministic parameter 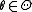 . The parameter space
. The parameter space 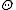 is partitioned into two disjoint sets
is partitioned into two disjoint sets 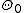 and
and 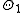 . Let
. Let  denote the hypothesis that
denote the hypothesis that  , and let
, and let 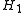 denote the hypothesis that
denote the hypothesis that 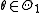 .
.The binary test of hypotheses is performed using a test function
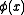 .
.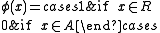
meaning that
 is in force if the measurement
is in force if the measurement 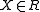 and that
and that  is in force if the measurement
is in force if the measurement 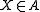 .
.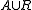 is a disjoint covering of the measurement space.
is a disjoint covering of the measurement space.Formal definition
A test function is UMP of size
is UMP of size  if for any other test function
if for any other test function 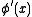 we have:
we have: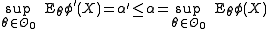
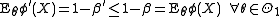
The Karlin-Rubin theorem
The Karlin-Rubin theorem can be regarded as an extension of the Neyman-Pearson lemma for composite hypotheses. Consider a scalar measurement having a probability density function parameterized by a scalar parameter θ, and define the likelihood ratio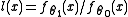 .
.If
 is monotone non-decreasing, in
is monotone non-decreasing, in  , for any pair
, for any pair 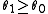 (meaning that the greater
(meaning that the greater  is, the more likely
is, the more likely  is), then the threshold test:
is), then the threshold test: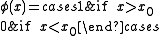

is the UMP test of size α for testing
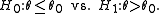
Note that exactly the same test is also UMP for testing

Important case: The exponential family
Although the Karlin-Rubin theorem may seem weak because of its restriction to scalar parameter and scalar measurement, it turns out that there exist a host of problems for which the theorem holds. In particular, the one-dimensional exponential familyExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
of probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s or probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
s with
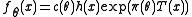
has a monotone non-decreasing likelihood ratio in the sufficient statistic
Sufficiency (statistics)
In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
T(x), provided that
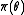 is non-decreasing.
is non-decreasing.Example
Let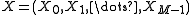 denote i.i.d. normally distributed
denote i.i.d. normally distributed 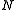 -dimensional random vectors with mean
-dimensional random vectors with mean 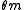 and covariance matrix
and covariance matrix 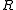 . We then have
. We then have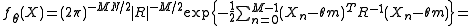

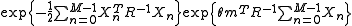
which is exactly in the form of the exponential family shown in the previous section, with the sufficient statistic being
Thus, we conclude that the test
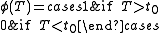
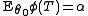
is the UMP test of size
 for testing
for testing 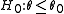 vs.
vs. 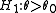
Further discussion
Finally, we note that in general, UMP tests do not exist for vector parameters or for two-sided tests (a test in which one hypothesis lies on both sides of the alternative). Why is it so?The reason is that in these situations, the most powerful test of a given size for one possible value of the parameter (e.g. for
 where
where 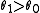 ) is different from the most powerful test of the same size for a different value of the parameter (e.g. for
) is different from the most powerful test of the same size for a different value of the parameter (e.g. for 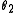 where
where 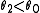 ). As a result, no test is uniformly most powerful.
). As a result, no test is uniformly most powerful.Further reading
- L. L. Scharf, Statistical Signal Processing, Addison-Wesley, 1991, section 4.7.