
Blum axioms
Encyclopedia
In computational complexity theory
the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable function
s. The axioms were first defined by Manuel Blum
in 1967.
Importantly, the Speedup
and Gap
theorems hold for any complexity measure satisfying these axioms. The most well-known measures satisfying these axioms are those of time (i.e., running time) and space (i.e., memory usage).
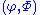 with
with  a Gödel numbering of the partial computable functions
a Gödel numbering of the partial computable functions 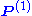 and a computable function
and a computable function
which satisfies the following Blum axioms. We write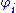 for the i-th partial computable function under the Gödel numbering
for the i-th partial computable function under the Gödel numbering 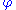 , and
, and 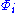 for the partial computable function
for the partial computable function 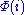 .
.
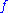 complexity class
complexity class
es of computable functions can be defined as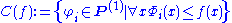
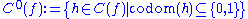
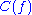 is the set of all computable functions with a complexity less than
is the set of all computable functions with a complexity less than  .
. 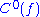 is the set of all boolean-valued function
is the set of all boolean-valued function
s with a complexity less than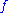 . If we consider those functions as indicator functions on sets,
. If we consider those functions as indicator functions on sets, 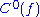 can be thought of as a complexity class of sets.
can be thought of as a complexity class of sets.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s. The axioms were first defined by Manuel Blum
Manuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
in 1967.
Importantly, the Speedup
Blum's speedup theorem
In computational complexity theory Blum's speedup theorem, first stated by Manuel Blum in 1967, is a fundamental theorem about the complexity of computable functions....
and Gap
Gap theorem
In computational complexity theory the Gap Theorem is a major theorem about the complexity of computable functions.It essentially states that there are arbitrarily large computable gaps in the hierarchy of complexity classes...
theorems hold for any complexity measure satisfying these axioms. The most well-known measures satisfying these axioms are those of time (i.e., running time) and space (i.e., memory usage).
Definitions
A Blum complexity measure is a tuple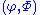 with
with  a Gödel numbering of the partial computable functions
a Gödel numbering of the partial computable functions 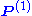 and a computable function
and a computable function
which satisfies the following Blum axioms. We write
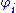 for the i-th partial computable function under the Gödel numbering
for the i-th partial computable function under the Gödel numbering 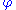 , and
, and 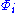 for the partial computable function
for the partial computable function 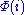 .
.
- the domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of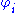 and the domain of
and the domain of 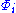 is identical.
is identical. - the set
 is recursiveRecursive languageIn mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
is recursiveRecursive languageIn mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
.
Examples
-
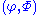 is a complexity measure, if
is a complexity measure, if 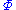 is either the time or the memory (or some suitable combination thereof) required for the computation coded by i.
is either the time or the memory (or some suitable combination thereof) required for the computation coded by i. -
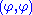 is not a complexity measure, since it fails the second axiom.
is not a complexity measure, since it fails the second axiom.
Complexity classes
For a total computable function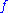 complexity class
complexity classComplexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es of computable functions can be defined as
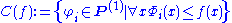
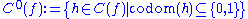
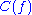 is the set of all computable functions with a complexity less than
is the set of all computable functions with a complexity less than  .
. 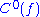 is the set of all boolean-valued function
is the set of all boolean-valued functionBoolean-valued function
A boolean-valued function, in some usages is a predicate or a proposition, is a function of the type f : X → B, where X is an arbitrary set and where B is a boolean domain....
s with a complexity less than
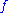 . If we consider those functions as indicator functions on sets,
. If we consider those functions as indicator functions on sets, 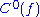 can be thought of as a complexity class of sets.
can be thought of as a complexity class of sets.

