
Algebraic statistics
Encyclopedia
Algebraic statistics is the use of algebra
to advance statistics
. Algebra has been useful for experimental design
, parameter estimation, and hypothesis testing.
Traditionally, algebraic statistics has been associated with the design of experiments
and multivariate analysis
(especially time series
). In recent years, the term "algebraic statistics" has been sometimes restricted, sometimes being used to label the use of algebraic geometry
and commutative algebra
in statistics.
s.
, and Rosemary A. Bailey
applied Abelian group
s to the design of experiments
. Experimental designs were also studied with affine geometry
over finite fields and then with the introduction of association scheme
s by R. C. Bose. Orthogonal array
s were introduced by C. R. Rao
also for experimental designs.
on locally compact group
s have long been used in statistical theory
, particularly in multivariate analysis
. Beurling
's factorization theorem
and much of the work on (abstract) harmonic analysis
sought better understanding of the Wold decomposition
of stationary stochastic processes, which is important in time series
statistics.
Encompassing previous results on probability theory on algebraic structures, Ulf Grenander
developed a theory of "abstract inference". Grenander's abstract inference and his theory of patterns
are useful for spatial statistics and image analysis
; these theories rely on lattice theory.
s and vector lattices
are used throughout statistical theory. Garrett Birkhoff
metrized the positive cone using Hilbert's projective metric
and proved Jentsch's theorem
using the contraction mapping
theorem. Birkhoff's results have been used for maximum entropy estimation
(which can be viewed as linear programming
in infinite dimensions) by Jonathan Borwein
and colleagues.
Vector lattice
s and conical measure
s were introduced into statistical decision theory by Lucien Le Cam
.
and commutative algebra
to study problems related to discrete random variables with finite state spaces. Commutative algebra and algebraic geometry have applications in statistics because many commonly used classes of discrete random variables can be viewed as algebraic varieties
.
X which can take on the values 0, 1, 2. Such a variable is completely characterized by the three probabilities
and these numbers clearly satisfy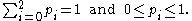
Conversely, any three such numbers unambiguously specify a random variable, so we can identify the random variable X with the tuple (p0,p1,p2)∈R3.
Now suppose X is a Binomial random variable with parameter p = 1 − q and n = 2, i.e. X represents the number of successes when repeating a certain experiment two times, where each experiment has an individual success probability of q. Then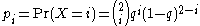
and it is not hard to show that the tuples (p0,p1,p2) which arise in this way are precisely the ones satisfying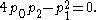
The latter is a polynomial equation defining an algebraic variety (or surface) in R3, and this variety, when intersected with the simplex
given by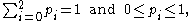
yields a piece of an algebraic curve
which may be identified with the set of all 3-state Bernoulli variables. Determining the parameter q amounts to locating one point on this curve; testing the hypothesis that a given variable X is Bernoulli amounts to testing whether a certain point lies on that curve or not.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
to advance statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. Algebra has been useful for experimental design
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, parameter estimation, and hypothesis testing.
Traditionally, algebraic statistics has been associated with the design of experiments
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
and multivariate analysis
Multivariate analysis
Multivariate analysis is based on the statistical principle of multivariate statistics, which involves observation and analysis of more than one statistical variable at a time...
(especially time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
). In recent years, the term "algebraic statistics" has been sometimes restricted, sometimes being used to label the use of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
in statistics.
The tradition of algebraic statistics
In the past, statisticians have used algebra to advance research in statistics. Some algebraic statistics led to the development of new topics in algebra and combinatorics, such as association schemeAssociation scheme
The theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
s.
Design of experiments
For example, Ronald A. Fisher, Henry B. MannHenry Mann
Henry Berthold Mann was a professor of mathematics and statistics at Ohio State University. Mann proved the Schnirelmann-Landau conjecture in number theory, and as a result earned the 1946 Cole Prize. He and his student developed the U-statistic of nonparametric statistics...
, and Rosemary A. Bailey
Rosemary A. Bailey
Rosemary A. Bailey is a British statistician who is renowned for her work in the design of experiments and the analysis of variance and in related areas of combinatorial design, especially in association schemes....
applied Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s to the design of experiments
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
. Experimental designs were also studied with affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
over finite fields and then with the introduction of association scheme
Association scheme
The theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
s by R. C. Bose. Orthogonal array
Orthogonal array
Orthogonal array testing is a black box testing technique which is a systematic, statistical way of software testing.It is used when the number of inputs to the system is relatively small, but too large to allow for exhaustive testing of every possible input to the systems...
s were introduced by C. R. Rao
C. R. Rao
Calyampudi Radhakrishna Rao FRS known as C R Rao is an Indian statistician. He is currently professor emeritus at Penn State University and Research Professor at the University at Buffalo. Rao has been honored by numerous colloquia, honorary degrees, and festschrifts and was awarded the US...
also for experimental designs.
Algebraic analysis and abstract statistical inference
Invariant measuresHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s have long been used in statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
, particularly in multivariate analysis
Multivariate analysis
Multivariate analysis is based on the statistical principle of multivariate statistics, which involves observation and analysis of more than one statistical variable at a time...
. Beurling
Arne Beurling
Arne Carl-August Beurling was a Swedish mathematician and professor of mathematics at Uppsala University and later at the Institute for Advanced Study in Princeton, New Jersey....
's factorization theorem
Invariant subspace
In mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
and much of the work on (abstract) harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
sought better understanding of the Wold decomposition
Wold decomposition
In operator theory, the Wold decomposition, named after Herman Wold, or Wold-von Neumann decomposition, after Wold and John von Neumann, is a classification theorem for isometric linear operators on a given Hilbert space...
of stationary stochastic processes, which is important in time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
statistics.
Encompassing previous results on probability theory on algebraic structures, Ulf Grenander
Ulf Grenander
Ulf Grenander is a statistician and a professor of applied mathematics at Brown University.His early research was in probability theory, stochastic processes, time series analysis, and statistical theory...
developed a theory of "abstract inference". Grenander's abstract inference and his theory of patterns
Pattern theory
Pattern theory, formulated by Ulf Grenander, is a mathematical formalism to describe knowledge of the world as patterns. It differs from other approaches to artificial intelligence in that it does not begin by prescribing algorithms and machinery to recognize and classify patterns; rather, it...
are useful for spatial statistics and image analysis
Image analysis
Image analysis is the extraction of meaningful information from images; mainly from digital images by means of digital image processing techniques...
; these theories rely on lattice theory.
Partially ordered sets and lattices
Partially ordered vector spaceOrdered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
s and vector lattices
Riesz space
In mathematics a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space where the order structure is a lattice....
are used throughout statistical theory. Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
metrized the positive cone using Hilbert's projective metric
Hilbert metric
In mathematics, the Hilbert metric, also known as the Hilbert projective metric, is an explicitly defined distance function on a bounded convex subset of the n-dimensional Euclidean space Rn...
and proved Jentsch's theorem
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
using the contraction mapping
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
theorem. Birkhoff's results have been used for maximum entropy estimation
Estimation
Estimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...
(which can be viewed as linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
in infinite dimensions) by Jonathan Borwein
Jonathan Borwein
Jonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
and colleagues.
Vector lattice
Riesz space
In mathematics a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space where the order structure is a lattice....
s and conical measure
Riesz space
In mathematics a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space where the order structure is a lattice....
s were introduced into statistical decision theory by Lucien Le Cam
Lucien le Cam
Lucien Marie Le Cam was a mathematician and statistician. He obtained a Ph.D. in 1952 at the University of California, Berkeley, was appointed Assistant Professor in 1953 and continued working there beyond his retirement in 1991 until his death.Le Cam was the major figure during the period 1950...
.
Recent work using commutative algebra and algebraic geometry
In recent years, the term "algebraic statistics" has been used more restrictively, to label the use of algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
to study problems related to discrete random variables with finite state spaces. Commutative algebra and algebraic geometry have applications in statistics because many commonly used classes of discrete random variables can be viewed as algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
Introductory example
Consider a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X which can take on the values 0, 1, 2. Such a variable is completely characterized by the three probabilities

and these numbers clearly satisfy
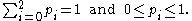
Conversely, any three such numbers unambiguously specify a random variable, so we can identify the random variable X with the tuple (p0,p1,p2)∈R3.
Now suppose X is a Binomial random variable with parameter p = 1 − q and n = 2, i.e. X represents the number of successes when repeating a certain experiment two times, where each experiment has an individual success probability of q. Then
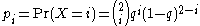
and it is not hard to show that the tuples (p0,p1,p2) which arise in this way are precisely the ones satisfying
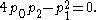
The latter is a polynomial equation defining an algebraic variety (or surface) in R3, and this variety, when intersected with the simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
given by
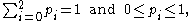
yields a piece of an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
which may be identified with the set of all 3-state Bernoulli variables. Determining the parameter q amounts to locating one point on this curve; testing the hypothesis that a given variable X is Bernoulli amounts to testing whether a certain point lies on that curve or not.
External links
- Journal of Algebraic StatisticsJournal of Algebraic Statistics

