
Wold decomposition
Encyclopedia
In operator theory
, the Wold decomposition, named after Herman Wold
, or Wold-von Neumann decomposition, after Wold and John von Neumann
, is a classification theorem for isometric linear operators
on a given Hilbert space
. It states that any isometry is a direct sums of copies of the unilateral shift and a unitary operator.
In time series analysis, the theorem implies that any stationary
discrete time stochastic process
can be decomposed into a pair of uncorrelated processes, one deterministic, and the other being a moving average process.
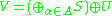
for some index set A, where S in the unilateral shift on a Hilbert space Hα, and U is an unitary operator (possible vacuous). The family {Hα} consists of isomorphic Hilbert spaces.
A proof can be sketched as follows. Successive applications of V give a descending sequences of copies of H isomorphically embedded in itself:
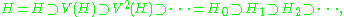
where V(H) denotes the range of V. The above defined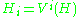 . If one defines
. If one defines
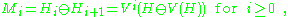
then
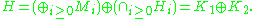
It is clear that K1 and K2 are invariant subspaces of V.
So V(K2) = K2. In other words, V restricted to K2 is a surjective isometry, i.e. an unitary operator U.
Furthermore, each Mi is isomorphic to another, with V being an isomorphicm between Mi and Mi+1: V "shifts" Mi to Mi+1. Suppose the dimension of each Mi is some cardinal number α. We see that K1 can be written as a direct sum Hilbert spaces

where each Hα is an invariant subspaces of V and V restricted to each Hα is the unilateral shift S. Therefore

which is a Wold decomposition of V.
of any proper, i.e. non-unitary, isometry is the unit disk in the complex plane.
An isometry V is said to be pure if, in the notation of the above proof, ∩i≥0 Hi = {0}. The multiplicity of a pure isometry V is the dimension of the kernel of V*, i.e. the cardinality of the index set A in the Wold decomposition of V. In other words, a pure isometry of multiplicity N takes the form
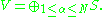
In this terminology, the Wold decomposition expresses an isometry as a direct sum of a pure isometry and an unitary.
A subspace M is called a wandering subspace
of V if Vn(M) ⊥ Vm(M) for all n ≠ m. In particular, each Mi defined above is a wandering subspace of V.
Let C(T) be the continuous functions on the unit circle T. We recall that the C*-algebra C*(S) generated by the unilateral shift S takes the following form
In this identification, S = Tz where z is the identity function in C(T). The algebra C*(S) is called the Toeplitz algebra
.
Theorem (Coburn) C*(V) is isomorphic to the Toeplitz algebra and V is the isomorphic image of Tz.
The proof hinges on the connections with C(T), in the description of the Toeplitz algebra and that the spectrum of an unitary operator is contained in the circle T.
The following properties of the Toeplitz algebra will be needed:
The Wold decomposition says that V is the direct sum of copies of Tz and then some unitary U:

So we invoke the continuous functional calculus
f → f(U), and define
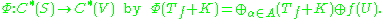
One can now verify Φ is an isomorphism that maps the unilateral shift to V:
By property 1 above, Φ is linear. The map Φ is injective because Tf is not compact for any non-zero f ∈ C(T) and thus Tf + K = 0 implies f = 0. Since the range of Φ is a C*-algebra, Φ is surjective by the minimality of C*(V). Property 2 and the continuous functional calculus ensure that Φ preserves the *-operation. Finally, the semicommutator property shows that Φ is multiplicative. Therefore the theorem holds.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, the Wold decomposition, named after Herman Wold
Herman Wold
Herman Ole Andreas Wold was a Norwegian-born econometrician and statistician who had a long career in Sweden...
, or Wold-von Neumann decomposition, after Wold and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, is a classification theorem for isometric linear operators
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
on a given Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. It states that any isometry is a direct sums of copies of the unilateral shift and a unitary operator.
In time series analysis, the theorem implies that any stationary
Stationary
Stationary can mean:* In statistics and probability: a stationary process.* In mathematics: a stationary point.* In mathematics: a stationary set.* In physics: a time-invariant quantity, such as a constant position or temperature....
discrete time stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
can be decomposed into a pair of uncorrelated processes, one deterministic, and the other being a moving average process.
Details
Let H be a Hilbert space, L(H) be the bounded operators on H, and V ∈ L(H) be an isometry. The Wold decomposition states that every isometry V takes the form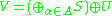
for some index set A, where S in the unilateral shift on a Hilbert space Hα, and U is an unitary operator (possible vacuous). The family {Hα} consists of isomorphic Hilbert spaces.
A proof can be sketched as follows. Successive applications of V give a descending sequences of copies of H isomorphically embedded in itself:
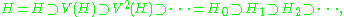
where V(H) denotes the range of V. The above defined
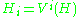 . If one defines
. If one defines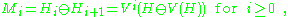
then
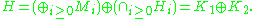
It is clear that K1 and K2 are invariant subspaces of V.
So V(K2) = K2. In other words, V restricted to K2 is a surjective isometry, i.e. an unitary operator U.
Furthermore, each Mi is isomorphic to another, with V being an isomorphicm between Mi and Mi+1: V "shifts" Mi to Mi+1. Suppose the dimension of each Mi is some cardinal number α. We see that K1 can be written as a direct sum Hilbert spaces

where each Hα is an invariant subspaces of V and V restricted to each Hα is the unilateral shift S. Therefore

which is a Wold decomposition of V.
Remarks
It is immediate from the Wold decomposition that the spectrumSpectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of any proper, i.e. non-unitary, isometry is the unit disk in the complex plane.
An isometry V is said to be pure if, in the notation of the above proof, ∩i≥0 Hi = {0}. The multiplicity of a pure isometry V is the dimension of the kernel of V*, i.e. the cardinality of the index set A in the Wold decomposition of V. In other words, a pure isometry of multiplicity N takes the form
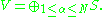
In this terminology, the Wold decomposition expresses an isometry as a direct sum of a pure isometry and an unitary.
A subspace M is called a wandering subspace
Wandering set
In those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system...
of V if Vn(M) ⊥ Vm(M) for all n ≠ m. In particular, each Mi defined above is a wandering subspace of V.
A sequence of isometries
The decomposition above can be generalized slightly to a sequence of isometries, indexed by the integers.The C*-algebra generated by an isometry
Consider an isometry V ∈ L(H). Denote by C*(V) the C*-algebra generated by V, i.e. C*(V) is the norm closure of polynomials in V and V*. The Wold decomposition can be applied to characterize C*(V).Let C(T) be the continuous functions on the unit circle T. We recall that the C*-algebra C*(S) generated by the unilateral shift S takes the following form
- C*(S) = {Tf + K | Tf is a Toeplitz operatorToeplitz operatorIn operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.- Details :Let S1 be the circle, with the standard Lebesgue measure, and L2 be the Hilbert space of square-integrable functions. A bounded measurable function g on S1 defines a...
with continuous symbol f ∈ C(T) and K is a compact operatorCompact operator on Hilbert spaceIn functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
}.
In this identification, S = Tz where z is the identity function in C(T). The algebra C*(S) is called the Toeplitz algebra
Toeplitz algebra
In operator algebras, the Toeplitz algebra is the C*-algebra generated by the unilateral shift on the Hilbert space l2. Taking l2 to be the Hardy space H2, the Toeplitz algebra consists of elements of the formT_f + K\;...
.
Theorem (Coburn) C*(V) is isomorphic to the Toeplitz algebra and V is the isomorphic image of Tz.
The proof hinges on the connections with C(T), in the description of the Toeplitz algebra and that the spectrum of an unitary operator is contained in the circle T.
The following properties of the Toeplitz algebra will be needed:
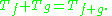
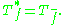
- The semicommutator
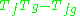 is compact.
is compact.
The Wold decomposition says that V is the direct sum of copies of Tz and then some unitary U:

So we invoke the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
f → f(U), and define
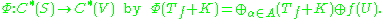
One can now verify Φ is an isomorphism that maps the unilateral shift to V:
By property 1 above, Φ is linear. The map Φ is injective because Tf is not compact for any non-zero f ∈ C(T) and thus Tf + K = 0 implies f = 0. Since the range of Φ is a C*-algebra, Φ is surjective by the minimality of C*(V). Property 2 and the continuous functional calculus ensure that Φ preserves the *-operation. Finally, the semicommutator property shows that Φ is multiplicative. Therefore the theorem holds.

