Tautological bundle
Encyclopedia
In mathematics
, tautological bundle is a term for a particularly natural vector bundle
occurring over a Grassmannian
, and more specially over projective space
. Canonical bundle as a name dropped out of favour, on the grounds that 'canonical' is heavily overloaded as it is, in mathematical terminology, and (worse) confusion with the canonical class in algebraic geometry
could scarcely be avoided.
Grassmannians by definition are the parameter spaces for linear subspace
s, of a given dimension, in a given vector space
W. If G is a Grassmannian, and Vg is the subspace of W corresponding to g in G, this is already almost the data required for a vector bundle: namely a vector space for each point g, varying continuously. All that can stop the definition of the tautological bundle from this indication, is the (pedantic) difficulty that the Vg are going to intersect. Fixing this up is a routine application of the disjoint union
device, so that the bundle projection is from a total space
made up of identical copies of the Vg, that now do not intersect. With this, we have the bundle.
The projective space case is included: see tautological line bundle. By convention and use P(V) may usefully carry the tautological bundle in the dual space
sense. That is, with V* the dual space, points of P(V) carry the vector subspaces of V* that are their kernels, when considered as (rays of) linear functional
s on V*. If V has dimension n + 1, the tautological line bundle
is one tautological bundle, and the other, just described, is of rank n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, tautological bundle is a term for a particularly natural vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
occurring over a Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
, and more specially over projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Canonical bundle as a name dropped out of favour, on the grounds that 'canonical' is heavily overloaded as it is, in mathematical terminology, and (worse) confusion with the canonical class in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
could scarcely be avoided.
Grassmannians by definition are the parameter spaces for linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
s, of a given dimension, in a given vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
W. If G is a Grassmannian, and Vg is the subspace of W corresponding to g in G, this is already almost the data required for a vector bundle: namely a vector space for each point g, varying continuously. All that can stop the definition of the tautological bundle from this indication, is the (pedantic) difficulty that the Vg are going to intersect. Fixing this up is a routine application of the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
device, so that the bundle projection is from a total space
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
made up of identical copies of the Vg, that now do not intersect. With this, we have the bundle.
The projective space case is included: see tautological line bundle. By convention and use P(V) may usefully carry the tautological bundle in the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
sense. That is, with V* the dual space, points of P(V) carry the vector subspaces of V* that are their kernels, when considered as (rays of) linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on V*. If V has dimension n + 1, the tautological line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
is one tautological bundle, and the other, just described, is of rank n.
Properties
- The Picard group of line bundles on
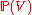is infinite cyclic, and the tautological line bundle is a generator. - In the case of projective space, where the tautological bundle is a line bundleLine bundleIn mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
, the associated invertible sheafInvertible sheafIn mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
of sections is
, the tensor inverse (ie the dual vector bundle) of the hyperplane bundle or Serre twist sheaf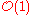 
; in other words the hyperplane bundle is the generator of the Picard group having positive degree (as a divisorDivisor (algebraic geometry)In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
) and the tautological bundle is its opposite: the generator of negative degree.