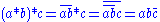Example of a non-associative algebra
Encyclopedia
This page presents and discusses an example of a non-associative division algebra
over the real number
s.
The multiplication is defined by taking the complex conjugate
of the usual multiplication: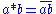 . This is a commutative, non-associative division algebra of dimension 2 over the reals, and has no unit element.
. This is a commutative, non-associative division algebra of dimension 2 over the reals, and has no unit element.
Proof that
For a proof that 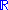 is a field
is a field
, see real number
.
Then, the complex numbers themselves clearly form a vector space
.
It remains to prove that the binary operation
given above satisfies the requirements of a division algebra
for all scalars a and b in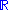 and all vectors x, y, and z (also in
and all vectors x, y, and z (also in  ).
).
For distributivity
:
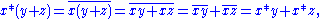
(similarly for right distributivity); and for the third and fourth requirements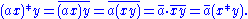
Non associativity of
So, if a, b, and c are all non-zero, and if a and c do not differ by a real multiple,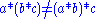 .
.
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
The multiplication is defined by taking the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the usual multiplication:
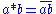 . This is a commutative, non-associative division algebra of dimension 2 over the reals, and has no unit element.
. This is a commutative, non-associative division algebra of dimension 2 over the reals, and has no unit element.Proof that 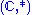 is a division algebra
is a division algebra
For a proof that 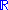 is a field
is a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, see real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
Then, the complex numbers themselves clearly form a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
It remains to prove that the binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
given above satisfies the requirements of a division algebra
- (x + y)z = x z + y z;
- x(y + z) = x y + x z;
- (a x)y = a(x y); and
- x(b y) = b(x y);
for all scalars a and b in
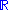 and all vectors x, y, and z (also in
and all vectors x, y, and z (also in  ).
).For distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
:
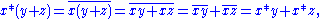
(similarly for right distributivity); and for the third and fourth requirements
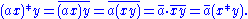
Non associativity of 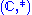
So, if a, b, and c are all non-zero, and if a and c do not differ by a real multiple,
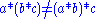 .
.