Activity (chemistry)
Encyclopedia
In chemical thermodynamics
, activity (symbol a) is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential
depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution
.
By convention, activity is treated as a dimensionless quantity
, although its actual value depends on customary choices of standard state
for the species. The activity of pure substances in condensed phases (solid or liquids) is normally taken as unity (the number 1). Activity depends on temperature, pressure and composition of the mixture, among other things. For gases, the effective partial pressure is usually referred to as fugacity
.
The difference between activity and other measures of composition arises because molecule
s in non-ideal gas
es or solution
s interact with each other, either to attract or to repel each other. The activity of an ion
is particularly influenced by its surroundings.
Activities should be used to define equilibrium constants but, in practice, concentration
s are often used instead. The same is often true of equations for reaction rate
s. However, there are circumstances where the activity and the concentration are significantly different and, as such, it is not valid to approximate with concentrations where activities are required. Two examples serve to illustrate this point:
where μi is the chemical potential
of the species under the conditions of interest, μoi is the chemical potential of that species in the chosen standard state
, R is the gas constant
and T is the thermodynamic temperature
. This definition can also be written in terms of the chemical potential:
Hence the activity will depend on any factor that alters the chemical potential. These include temperature, pressure, chemical environment etc. In specialised cases, other factors may have to be considered, such as the presence of an electric or magnetic field or the position in a gravitational field. However the most common use of activity is to describe the variation in chemical potential with the composition of a mixture.
The activity also depends on the choice of standard state, as it describes the difference between an actual chemical potential and a standard chemical potential. In principle, the choice of standard state is arbitrary, although there are certain conventional standard states which are usually used in different situations.
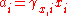
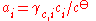
The division by the standard molality mo or the standard amount concentration co is necessary to ensure that both the activity and the activity coefficient are dimensionless, as is conventional.
When the activity coefficient is close to one, the substance shows almost ideal behaviour according to Henry's law
. In these cases, the activity can be substituted with the appropriate dimensionless measure of composition xi, mi/mo or ci/co. It is also possible to define an activity coefficient in terms of Raoult's law: the International Union of Pure and Applied Chemistry
(IUPAC) recommends the symbol ƒ for this activity coefficient, although this should not be confused with fugacity
.
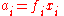. Solution can also become too diluted when necessary.
ƒi: this may be higher or lower than its mechanical pressure. By historical convention, fugacities have the dimension of pressure, so the dimensionless activity is given by:
where φi is the dimensionless fugacity coefficient of the species, xi is its fraction in the gaseous mixture (x = 1 for a pure gas) and p is the total pressure. The value po is the standard pressure: it may be equal to 1 atm (101.325 kPa) or 1 bar (100 kPa) depending on the source of data, and should always be quoted.
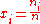
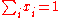
The standard state of each component in the mixture is taken to be the pure substance, i.e. the pure substance has an activity of one. When activity coefficients are used, they are usually defined in terms of Raoult's law,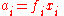
where ƒi is the Raoult's law activity coefficient: an activity coefficient of one indicates ideal behaviour according to Raoult's law.
rather than Raoult's law, and it is more usual to express the composition of the solution in terms of the amount concentration c (in mol/L) or the molality m (in mol/kg) of the solute rather than in amount fractions. The standard state of a dilute solution is a hypothetical solution of concentration co = 1 mol/L (or molality mo = 1 mol/kg) which shows ideal behaviour (also referred to as "infinite-dilution" behaviour). The standard state, and hence the activity, depends on which measure of composition is used. Molalities are often preferred as the volumes of non-ideal mixtures are not strictly additive and are also temperature-dependent: molalities do not depend on volume, whereas amount concentrations do.
The activity of the solute is given by: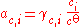
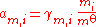
It should be noted however that in a liquid solution the activity coefficient of a given ion
(e.g. Ca2+) isn't measurable because it is experimentally impossible to independently measure the electrochemical potential of an ion in solution. (We cannot add cations without putting in anions at the same time). Therefore one introduces the notions of
mean ionic activity
mean ionic molality
mean ionic activity coefficient
where ν = ν+ + ν– represent the stoichiometric coefficients involved in the ionic dissociation process
Even though γ+ and γ– cannot be determined separately, γ± is a measureable quantity that can also be predicted for sufficiently dilute systems using Debye–Hückel theory
. For the activity of a strong ionic solute (complete dissociation) we can write:
Another way to determine the activity of a species is through the manipulation of colligative properties
, specifically freezing point depression. Using freezing point depression techniques, it is possible to calculate the activity of a weak acid from the relation,
where m is the total molal equilibrium concentration of solute determined by any colligative property measurement(in this case ΔTfus, m is the nominal molality obtained from titration and a is the activity of the species.
There are also electrochemical methods that allow the determination of activity and its coefficient.
The value of the mean ionic activity coefficient γ± of ion
s in solution can also be estimated with the Debye–Hückel equation, the Davies equation
or the Pitzer equations
.
s, where the chemical potential depends on the temperature
T, pressure
p and the activity ai according to the formula
:
where R is the gas constant
and µio is the value of µi under standard conditions.
Formulae involving activities can be simplified by considering that:
Therefore, it is approximately equal to its concentration.
The latter follows from any definition based on Raoult's law, because if we let the solute concentration x1 go to zero, the vapor pressure of the solvent p will go to p*. Thus its activity a = p/p* will go to unity. This means that if during a reaction in dilute solution more solvent is generated (the reaction produces water e.g.) we can typically set its activity to unity.
Solid and liquid activities do not depend very strongly on pressure because their molar volumes are typically small. Graphite
at 100 bars has an activity of only 1.01 if we choose po = 1 bar as standard state. Only at very high pressures do we need to worry about such changes.Changes can also come as a result of too much dilution of solution.
in aqueous solution are given in the table. In an ideal solution, these values would all be unity. The deviations tend to become larger with increasing molality and temperature, but with some exceptions.
Chemical thermodynamics
Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics...
, activity (symbol a) is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution
Ideal solution
In chemistry, an ideal solution or ideal mixture is a solution with thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of solution is zero as is the volume change on mixing; the closer to zero the enthalpy of solution is, the more "ideal" the behavior of the...
.
By convention, activity is treated as a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
, although its actual value depends on customary choices of standard state
Standard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
for the species. The activity of pure substances in condensed phases (solid or liquids) is normally taken as unity (the number 1). Activity depends on temperature, pressure and composition of the mixture, among other things. For gases, the effective partial pressure is usually referred to as fugacity
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
.
The difference between activity and other measures of composition arises because molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s in non-ideal gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es or solution
Solution
In chemistry, a solution is a homogeneous mixture composed of only one phase. In such a mixture, a solute is dissolved in another substance, known as a solvent. The solvent does the dissolving.- Types of solutions :...
s interact with each other, either to attract or to repel each other. The activity of an ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
is particularly influenced by its surroundings.
Activities should be used to define equilibrium constants but, in practice, concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
s are often used instead. The same is often true of equations for reaction rate
Reaction rate
The reaction rate or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place...
s. However, there are circumstances where the activity and the concentration are significantly different and, as such, it is not valid to approximate with concentrations where activities are required. Two examples serve to illustrate this point:
- In a solution of potassium hydrogen iodate at 0.02 M the activity is 40% lower than the calculated hydrogen ion concentration, resulting in a much higher pHPHIn chemistry, pH is a measure of the acidity or basicity of an aqueous solution. Pure water is said to be neutral, with a pH close to 7.0 at . Solutions with a pH less than 7 are said to be acidic and solutions with a pH greater than 7 are basic or alkaline...
than expected. - When a 0.1 M hydrochloric acidHydrochloric acidHydrochloric acid is a solution of hydrogen chloride in water, that is a highly corrosive, strong mineral acid with many industrial uses. It is found naturally in gastric acid....
solution containing methyl green indicatorPH indicatorA pH indicator is a halochromic chemical compound that is added in small amounts to a solution so that the pH of the solution can be determined visually. Hence a pH indicator is a chemical detector for hydronium ions or hydrogen ions in the Arrhenius model. Normally, the indicator causes the...
is added to a 5 M solution of magnesium chlorideMagnesium chlorideMagnesium chloride is the name for the chemical compounds with the formulas MgCl2 and its various hydrates MgCl2x. These salts are typical ionic halides, being highly soluble in water. The hydrated magnesium chloride can be extracted from brine or sea water...
, the color of the indicator changes from green to yellow—indicating increasing acidity—when in fact the acid has been diluted. Although at low ionic strength (<0.1 M) the activity coefficientActivity coefficientAn activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
approaches unity, this coefficient can actually increase with ionic strength in a high ionic strength regime. For hydrochloric acid solutions, the minimum is around 0.4 M.
Definition
The activity of a species i, denoted ai, is defined as:where μi is the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the species under the conditions of interest, μ
Standard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
, R is the gas constant
Gas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
and T is the thermodynamic temperature
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
. This definition can also be written in terms of the chemical potential:
Hence the activity will depend on any factor that alters the chemical potential. These include temperature, pressure, chemical environment etc. In specialised cases, other factors may have to be considered, such as the presence of an electric or magnetic field or the position in a gravitational field. However the most common use of activity is to describe the variation in chemical potential with the composition of a mixture.
The activity also depends on the choice of standard state, as it describes the difference between an actual chemical potential and a standard chemical potential. In principle, the choice of standard state is arbitrary, although there are certain conventional standard states which are usually used in different situations.
Activity coefficient
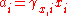
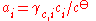
The activity coefficient γ, which is also a dimensionless quantity, relates the activity to a measured amount fraction xi, molality mi or amount concentration ci:The division by the standard molality m
When the activity coefficient is close to one, the substance shows almost ideal behaviour according to Henry's law
Henry's law
In physics, Henry's law is one of the gas laws formulated by William Henry in 1803. It states that:An equivalent way of stating the law is that the solubility of a gas in a liquid at a particular temperature is proportional to the pressure of that gas above the liquid...
. In these cases, the activity can be substituted with the appropriate dimensionless measure of composition xi, mi/m
International Union of Pure and Applied Chemistry
The International Union of Pure and Applied Chemistry is an international federation of National Adhering Organizations that represents chemists in individual countries. It is a member of the International Council for Science . The international headquarters of IUPAC is located in Zürich,...
(IUPAC) recommends the symbol ƒ for this activity coefficient, although this should not be confused with fugacity
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
.
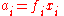. Solution can also become too diluted when necessary.Gases
In most laboratory situations, the difference in behaviour between a real gas and an ideal gas is dependent only on the pressure and the temperature, not on the presence of any other gases. At a given temperature, the "effective" pressure of a gas i is given by its fugacityFugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
ƒi: this may be higher or lower than its mechanical pressure. By historical convention, fugacities have the dimension of pressure, so the dimensionless activity is given by:
where φi is the dimensionless fugacity coefficient of the species, xi is its fraction in the gaseous mixture (x = 1 for a pure gas) and p is the total pressure. The value p
Mixtures in general
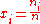
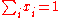
The most convenient way of expressing the composition of a generic mixture is by using the amount fractions x of the different components, whereThe standard state of each component in the mixture is taken to be the pure substance, i.e. the pure substance has an activity of one. When activity coefficients are used, they are usually defined in terms of Raoult's law,
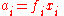
where ƒi is the Raoult's law activity coefficient: an activity coefficient of one indicates ideal behaviour according to Raoult's law.
Dilute solutions (non-ionic)
A solute in dilute solution usually follows Henry's lawHenry's law
In physics, Henry's law is one of the gas laws formulated by William Henry in 1803. It states that:An equivalent way of stating the law is that the solubility of a gas in a liquid at a particular temperature is proportional to the pressure of that gas above the liquid...
rather than Raoult's law, and it is more usual to express the composition of the solution in terms of the amount concentration c (in mol/L) or the molality m (in mol/kg) of the solute rather than in amount fractions. The standard state of a dilute solution is a hypothetical solution of concentration c
The activity of the solute is given by:
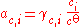
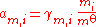
Ionic solutions
When the solute undergoes ionic dissociation in solution (a salt e.g.), the system becomes decidedly non-ideal and we need to take the dissociation process into consideration. We can define activities for the cations and anions separately (a+ and a–).It should be noted however that in a liquid solution the activity coefficient of a given ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
(e.g. Ca2+) isn't measurable because it is experimentally impossible to independently measure the electrochemical potential of an ion in solution. (We cannot add cations without putting in anions at the same time). Therefore one introduces the notions of
mean ionic activity
- a±ν = a+ν+a–ν–
mean ionic molality
- m±ν = m+ν+m–ν–
mean ionic activity coefficient
- γ±ν = γ+ν+γ–ν–
where ν = ν+ + ν– represent the stoichiometric coefficients involved in the ionic dissociation process
Even though γ+ and γ– cannot be determined separately, γ± is a measureable quantity that can also be predicted for sufficiently dilute systems using Debye–Hückel theory
Debye–Hückel theory
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes. It was based on an extremely simplified model of the electrolyte solution but nevertheless gave accurate predictions of mean activity...
. For the activity of a strong ionic solute (complete dissociation) we can write:
- a2 = a±ν = γ±νm±ν
Measurement
The most direct way of measuring an activity of a species is to measure its partial vapor pressure in equilibrium with a number of solutions of different strength. For some solutes this is not practical, say sucrose or salt (NaCl) do not have a measurable vapor pressure at ordinary temperatures. However, in such cases it is possible to measure the vapor pressure of the solvent instead. Using the Gibbs–Duhem relation it is possible to translate the change in solvent vapor pressures with concentration into activities for the solute.Another way to determine the activity of a species is through the manipulation of colligative properties
Colligative properties
Colligative properties are properties of solutions that depend on the number of molecules in a given volume of solvent and not on the properties/identity of the molecules. Colligative properties include: relative lowering of vapor pressure; elevation of boiling point; depression of freezing point...
, specifically freezing point depression. Using freezing point depression techniques, it is possible to calculate the activity of a weak acid from the relation,
where m is the total molal equilibrium concentration of solute determined by any colligative property measurement(in this case ΔTfus, m is the nominal molality obtained from titration and a is the activity of the species.
There are also electrochemical methods that allow the determination of activity and its coefficient.
The value of the mean ionic activity coefficient γ± of ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s in solution can also be estimated with the Debye–Hückel equation, the Davies equation
Davies equation
The Davies equation is an empirical extension of Debye–Hückel theory which can be used to calculate activity coefficients of electrolyte solutions at relatively high concentrations. The equation, originally published in 1938, was refined by fitting to experimental data...
or the Pitzer equations
Pitzer equations
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise...
.
Use
Chemical activities should be used to define chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
s, where the chemical potential depends on the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
T, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
p and the activity ai according to the formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
:
where R is the gas constant
Gas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
and µi
Formulae involving activities can be simplified by considering that:
- For a chemical solution:
- the solventSolventA solvent is a liquid, solid, or gas that dissolves another solid, liquid, or gaseous solute, resulting in a solution that is soluble in a certain volume of solvent at a specified temperature...
has an activity of unity - At a low concentration, the activity of a solute can be approximated to the ratio of its concentration over the standard concentration:
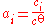
- the solvent
Therefore, it is approximately equal to its concentration.
- For a mix of gasGasGas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
at low pressure, the activity is equal to the ratio of the partial pressurePartial pressureIn a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture....
of the gas over the standard pressure:
-
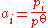
- Therefore, it is equal to the partial pressure in barsBar (unit)The bar is a unit of pressure equal to 100 kilopascals, and roughly equal to the atmospheric pressure on Earth at sea level. Other units derived from the bar are the megabar , kilobar , decibar , centibar , and millibar...
(compared to a standard pressure of 1 bar).
- For a solid body, a uniform, single species solid at one bar has an activity of unity. The same thing holds for a pure liquid.
The latter follows from any definition based on Raoult's law, because if we let the solute concentration x1 go to zero, the vapor pressure of the solvent p will go to p*. Thus its activity a = p/p* will go to unity. This means that if during a reaction in dilute solution more solvent is generated (the reaction produces water e.g.) we can typically set its activity to unity.
Solid and liquid activities do not depend very strongly on pressure because their molar volumes are typically small. Graphite
Graphite
The mineral graphite is one of the allotropes of carbon. It was named by Abraham Gottlob Werner in 1789 from the Ancient Greek γράφω , "to draw/write", for its use in pencils, where it is commonly called lead . Unlike diamond , graphite is an electrical conductor, a semimetal...
at 100 bars has an activity of only 1.01 if we choose p
Example values
Example values of activity coefficients of sodium chlorideSodium chloride
Sodium chloride, also known as salt, common salt, table salt or halite, is an inorganic compound with the formula NaCl. Sodium chloride is the salt most responsible for the salinity of the ocean and of the extracellular fluid of many multicellular organisms...
in aqueous solution are given in the table. In an ideal solution, these values would all be unity. The deviations tend to become larger with increasing molality and temperature, but with some exceptions.
| Molality (mol/kg) | 25 °C | 50 °C | 100 °C | 200 °C | 300 °C | 350 °C |
|---|---|---|---|---|---|---|
| 0.05 | 0.820 | 0.814 | 0.794 | 0.725 | 0.592 | 0.473 |
| 0.50 | 0.680 | 0.675 | 0.644 | 0.619 | 0.322 | 0.182 |
| 2.00 | 0.669 | 0.675 | 0.641 | 0.450 | 0.212 | 0.074 |
| 5.00 | 0.873 | 0.886 | 0.803 | 0.466 | 0.167 | 0.044 |
See also
- FugacityFugacityIn chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
, the equivalent of activity for partial pressurePartial pressureIn a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture.... - Chemical equilibriumChemical equilibriumIn a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
- Electrochemical potential
- Excess chemical potentialExcess chemical potentialThe excess chemical potential is defined as the difference between the chemical potential of a given species and that of an ideal gas under the same conditions ....
- Partial molar propertyPartial molar propertyA partial molar property is a thermodynamic quantity which indicates how an extensive property of a solution or mixture varies with changes in the molar composition of the mixture at constant temperature and pressure, or for constant values of the natural variables of the extensive property...
- Thermodynamic equilibriumThermodynamic equilibriumIn thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...