
Fugacity
Encyclopedia
In chemical thermodynamics
, the fugacity (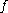 ) of a real gas
) of a real gas
is an effective pressure
which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas
which has the same chemical potential
as the real gas. For example, nitrogen gas (N2) at 0°C and a pressure of 100 atm has a fugacity of 97.03 atm. This means that the chemical potential of real nitrogen at a pressure of 100 atm has the value which ideal nitrogen would have at a pressure of 97.03 atm.
Fugacities are determined experimentally or estimated for various models such as a Van der Waals gas that are closer to reality than an ideal gas. The ideal gas pressure and fugacity are related through the dimensionless fugacity coefficient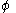 .
.
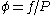
For nitrogen at 100 atm, the fugacity coefficient is 97.03 atm / 100 atm = 0.9703. For an ideal gas, fugacity and pressure are equal so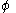 is 1.
is 1.
The fugacity is closely related to the thermodynamic activity
. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference pressure is called the standard state
and normally chosen as 1 atmosphere
or 1 bar
, Again using nitrogen at 100 atm as an example, since the fugacity is 97.03 atm, the activity is just 97.03 with no units.
Accurate calculations of chemical equilibrium
for real gases should use the fugacity rather than the pressure. The thermodynamic condition for chemical equilibrium is that the total chemical potential of reactants is equal to that of products. If the chemical potential of each gas is expressed as a function of fugacity, the equilibrium condition may be transformed into the familiar reaction quotient
form (or law of mass action) except that the pressures are replaced by fugacities.
For a condensed phase (liquid or solid), the chemical potential is equal to that of the vapor in equilibrium with the condensed phase, and therefore the fugacity is equal to the fugacity of the vapor. This fugacity is approximately equal to the vapor pressure
when the vapor pressure is not too high.
The word "fugacity" is derived from the Latin for "fleetness", which is often interpreted as “the tendency to flee or escape”. The concept of fugacity was introduced by American chemist Gilbert N. Lewis
.
For any pure substance, the chemical potential (μ) is equal to the molar Gibbs free energy
, whose variation with temperature (T) and pressure (p) is given by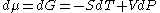 . At constant temperature, this expression can be integrated as a function of
. At constant temperature, this expression can be integrated as a function of 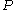 . We must also set a reference state
. We must also set a reference state
. For an ideal gas the reference state depends only on pressure, and we set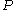 = 1 bar
= 1 bar
so that
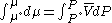
Now, for an ideal gas
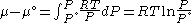
Reordering, we get
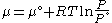
This gives the chemical potential for an ideal gas in an isothermal process, with a reference state is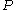 = 1 bar.
= 1 bar.
For a real gas, we cannot calculate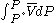 because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equation
because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equation
, the Redlich-Kwong or any other equation of state
, it would depend on the substance being studied and would be therefore of very limited utility.
We would like the expression for a real gas’ chemical potential to be similar to the one for an ideal gas. We therefore define a magnitude, called fugacity, so that the chemical potential for a real gas becomes
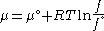
with a given reference state to be discussed later. This is the usual form of the definition, but it may be solved for f to obtain the equivalent explicit form
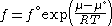
. Yet fugacity allows the use of many of the relationships developed for an idealized system.
In the real world, gases approach ideal gas
behavior at low pressures and high temperatures; under such conditions the value of fugacity approaches the value of pressure
. Yet no substance is truly ideal. At moderate pressures real gases have attractive interactions and at high pressures intermolecular repulsions become important. Both interactions result in a deviation from "ideal" behavior for which interactions between gas atoms or molecules are ignored.
For a given temperature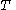 , the fugacity
, the fugacity 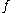 satisfies the following differential relation:
satisfies the following differential relation:
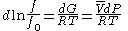
where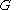 is the Gibbs free energy
is the Gibbs free energy
,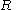 is the gas constant
is the gas constant
,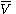 is the fluid's molar volume
is the fluid's molar volume
, and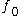 is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when
is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when 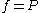 , this equation reduces to the ideal gas law
, this equation reduces to the ideal gas law
.
Thus, for any two physical states at the same temperature, represented by subscripts 1 and 2, the ratio of the two fugacities is as follows:

For an ideal gas, this becomes simply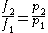 or
or 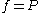
But for , every gas is an ideal gas. Therefore, fugacity must obey the limit
, every gas is an ideal gas. Therefore, fugacity must obey the limit
equation

We determine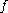 by defining a function
by defining a function
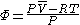
We can obtain values for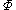 experimentally easily by measuring
experimentally easily by measuring 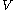 ,
,  and
and 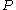 .
.
From the expression above we have

We can then write
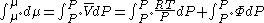
Where
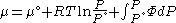
Since the expression for an ideal gas was chosen to be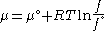 ,we must have
,we must have
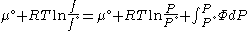
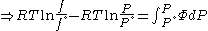
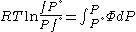
Suppose we choose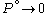 . Since
. Since 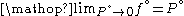 , we obtain
, we obtain

The fugacity coefficient is defined as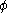 = f/P (note that for an ideal gas,
= f/P (note that for an ideal gas, 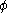 = 1.0), and
= 1.0), and
it will then verify
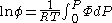
The integral can be evaluated via graphical integration if we experimentally measure values for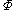 while varying
while varying 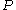 .
.
We can then find the fugacity coefficient of a gas at a given pressure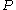 and calculate
and calculate
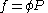
The reference state for the expression of a real gas’ chemical potential is taken to be “ideal gas, at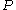 = 1 bar and temperature
= 1 bar and temperature 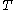 ”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
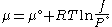
Chemical thermodynamics
Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics...
, the fugacity (
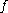 ) of a real gas
) of a real gasReal gas
Real gases – as opposed to a perfect or ideal gas – exhibit properties that cannot be explained entirely using the ideal gas law. To understand the behaviour of real gases, the following must be taken into account:* compressibility effects;...
is an effective pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
which has the same chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
as the real gas. For example, nitrogen gas (N2) at 0°C and a pressure of 100 atm has a fugacity of 97.03 atm. This means that the chemical potential of real nitrogen at a pressure of 100 atm has the value which ideal nitrogen would have at a pressure of 97.03 atm.
Fugacities are determined experimentally or estimated for various models such as a Van der Waals gas that are closer to reality than an ideal gas. The ideal gas pressure and fugacity are related through the dimensionless fugacity coefficient
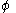 .
.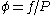
For nitrogen at 100 atm, the fugacity coefficient is 97.03 atm / 100 atm = 0.9703. For an ideal gas, fugacity and pressure are equal so
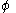 is 1.
is 1.The fugacity is closely related to the thermodynamic activity
Activity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference pressure is called the standard state
Standard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
and normally chosen as 1 atmosphere
Atmosphere (unit)
The standard atmosphere is an international reference pressure defined as 101325 Pa and formerly used as unit of pressure. For practical purposes it has been replaced by the bar which is 105 Pa...
or 1 bar
Bar (unit)
The bar is a unit of pressure equal to 100 kilopascals, and roughly equal to the atmospheric pressure on Earth at sea level. Other units derived from the bar are the megabar , kilobar , decibar , centibar , and millibar...
, Again using nitrogen at 100 atm as an example, since the fugacity is 97.03 atm, the activity is just 97.03 with no units.
Accurate calculations of chemical equilibrium
Chemical equilibrium
In a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
for real gases should use the fugacity rather than the pressure. The thermodynamic condition for chemical equilibrium is that the total chemical potential of reactants is equal to that of products. If the chemical potential of each gas is expressed as a function of fugacity, the equilibrium condition may be transformed into the familiar reaction quotient
Reaction quotient
In chemistry, a reaction quotient: Qr is a function of the activities or concentrations of the chemical species involved in a chemical reaction. In the special case that the reaction is at equilibrium the reaction quotient is equal to the equilibrium constant....
form (or law of mass action) except that the pressures are replaced by fugacities.
For a condensed phase (liquid or solid), the chemical potential is equal to that of the vapor in equilibrium with the condensed phase, and therefore the fugacity is equal to the fugacity of the vapor. This fugacity is approximately equal to the vapor pressure
Vapor pressure
Vapor pressure or equilibrium vapor pressure is the pressure of a vapor in thermodynamic equilibrium with its condensed phases in a closed system. All liquids have a tendency to evaporate, and some solids can sublimate into a gaseous form...
when the vapor pressure is not too high.
The word "fugacity" is derived from the Latin for "fleetness", which is often interpreted as “the tendency to flee or escape”. The concept of fugacity was introduced by American chemist Gilbert N. Lewis
Gilbert N. Lewis
Gilbert Newton Lewis was an American physical chemist known for the discovery of the covalent bond , his purification of heavy water, his reformulation of chemical thermodynamics in a mathematically rigorous manner accessible to ordinary chemists, his theory of Lewis acids and...
.
Definition in terms of chemical potential
The fugacity of a real gas is formally defined by an equation analogous to the relation between the chemical potential and the pressure of an ideal gas.For any pure substance, the chemical potential (μ) is equal to the molar Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
, whose variation with temperature (T) and pressure (p) is given by
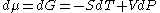 . At constant temperature, this expression can be integrated as a function of
. At constant temperature, this expression can be integrated as a function of 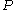 . We must also set a reference state
. We must also set a reference stateStandard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
. For an ideal gas the reference state depends only on pressure, and we set
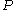 = 1 bar
= 1 barBar (unit)
The bar is a unit of pressure equal to 100 kilopascals, and roughly equal to the atmospheric pressure on Earth at sea level. Other units derived from the bar are the megabar , kilobar , decibar , centibar , and millibar...
so that
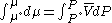
Now, for an ideal gas

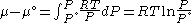
Reordering, we get
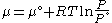
This gives the chemical potential for an ideal gas in an isothermal process, with a reference state is
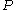 = 1 bar.
= 1 bar.For a real gas, we cannot calculate
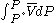 because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equation
because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equationVan der Waals equation
The van der Waals equation is an equation of state for a fluid composed of particles that have a non-zero volume and a pairwise attractive inter-particle force It was derived by Johannes Diderik van der Waals in 1873, who received the Nobel prize in 1910 for "his work on the equation of state for...
, the Redlich-Kwong or any other equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
, it would depend on the substance being studied and would be therefore of very limited utility.
We would like the expression for a real gas’ chemical potential to be similar to the one for an ideal gas. We therefore define a magnitude, called fugacity, so that the chemical potential for a real gas becomes
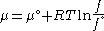
with a given reference state to be discussed later. This is the usual form of the definition, but it may be solved for f to obtain the equivalent explicit form
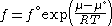
Evaluation of fugacity for a real gas
Fugacity is used to better approximate the chemical potential of real gases than estimations made using the ideal gas lawIdeal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
. Yet fugacity allows the use of many of the relationships developed for an idealized system.
In the real world, gases approach ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
behavior at low pressures and high temperatures; under such conditions the value of fugacity approaches the value of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. Yet no substance is truly ideal. At moderate pressures real gases have attractive interactions and at high pressures intermolecular repulsions become important. Both interactions result in a deviation from "ideal" behavior for which interactions between gas atoms or molecules are ignored.
For a given temperature
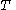 , the fugacity
, the fugacity 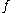 satisfies the following differential relation:
satisfies the following differential relation: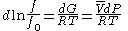
where
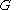 is the Gibbs free energy
is the Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
,
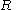 is the gas constant
is the gas constantGas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
,
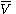 is the fluid's molar volume
is the fluid's molar volumeMolar volume
The molar volume, symbol Vm, is the volume occupied by one mole of a substance at a given temperature and pressure. It is equal to the molar mass divided by the mass density...
, and
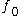 is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when
is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when 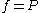 , this equation reduces to the ideal gas law
, this equation reduces to the ideal gas lawIdeal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
.
Thus, for any two physical states at the same temperature, represented by subscripts 1 and 2, the ratio of the two fugacities is as follows:

For an ideal gas, this becomes simply
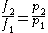 or
or 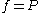
But for
 , every gas is an ideal gas. Therefore, fugacity must obey the limit
, every gas is an ideal gas. Therefore, fugacity must obey the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
equation

We determine
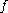 by defining a function
by defining a function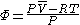
We can obtain values for
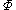 experimentally easily by measuring
experimentally easily by measuring 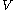 ,
,  and
and 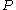 .
.From the expression above we have

We can then write
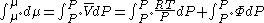
Where
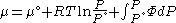
Since the expression for an ideal gas was chosen to be
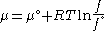 ,we must have
,we must have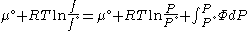
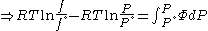
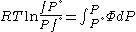
Suppose we choose
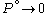 . Since
. Since 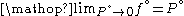 , we obtain
, we obtain
The fugacity coefficient is defined as
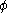 = f/P (note that for an ideal gas,
= f/P (note that for an ideal gas, 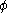 = 1.0), and
= 1.0), andit will then verify
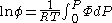
The integral can be evaluated via graphical integration if we experimentally measure values for
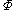 while varying
while varying 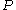 .
.We can then find the fugacity coefficient of a gas at a given pressure
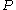 and calculate
and calculate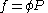
The reference state for the expression of a real gas’ chemical potential is taken to be “ideal gas, at
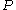 = 1 bar and temperature
= 1 bar and temperature 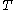 ”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas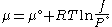
See also
- Activity (chemistry)Activity (chemistry)In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
, the measure of the “effective concentration” of a species in a mixture - Chemical equilibriumChemical equilibriumIn a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
- Electrochemical potential
- Excess chemical potentialExcess chemical potentialThe excess chemical potential is defined as the difference between the chemical potential of a given species and that of an ideal gas under the same conditions ....
- Partial molar propertyPartial molar propertyA partial molar property is a thermodynamic quantity which indicates how an extensive property of a solution or mixture varies with changes in the molar composition of the mixture at constant temperature and pressure, or for constant values of the natural variables of the extensive property...
- Thermodynamic equilibriumThermodynamic equilibriumIn thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
- Fugacity capacityFugacity capacityThe fugacity capacity constant is used to help describe the concentration of a chemical in a system . Hemond and Hechner-Levy describe how to utilize the fugacity capacity to calculate the concentration of a chemical in a system. Depending on the chemical, fugacity capacity varies...

