
Whitney topologies
Encyclopedia
In mathematics, and especially differential topology
, functional analysis
and singularity theory, the Whitney topologies are a countably infinite family of topologies defined on the set of smooth mappings between two smooth manifolds. They are named after the American mathematician Hassler Whitney
.
s of all orders exist and are continuous
.
, let Jk(M,N) denote the k-jet space
of mappings between M and N. The jet space can be endowed with a smooth structure (i.e. a structure as a C∞ manifold) which make it into a topological space. This topology is used to define a topology on C∞(M,N).
For a fixed integer
consider an open subset and denote by Sk(U) the following: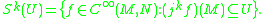
The sets Sk(U) form a basis for the Whitney Ck-topology on C∞(M,N).
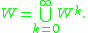
s, with real coefficients, in m variables and of order at most k. This is a real vector space
with dimension
Writing } then, by the standard theory of vector spaces and so is a real, finite dimensional manifold. Next, define:
Using b to denote the dimension Bkm,n, we see that , and so is a real, finite dimensional manifold.
In fact, if M and N have dimension m and n respectively then:
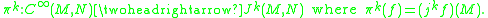
In the Whitney Ck-topology the open sets in C∞(M,N) are, by definition, the preimages of open sets in Jk(M,N). It follows that the map πk between C∞(M,N) given the Whitney Ck-topology and Jk(M,N) given the Euclidean topology is continuous.
Given the Whitney C∞-topology, the space C∞(M,N) is a Baire space
, i.e. every residual set is dense.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and singularity theory, the Whitney topologies are a countably infinite family of topologies defined on the set of smooth mappings between two smooth manifolds. They are named after the American mathematician Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
.
Construction
Let M and N be two real, smooth manifolds. Furthermore, let C∞(M,N) denote the space of smooth mappings between M and N. The notation C∞ means that the mappings are infinitely differentiable, i.e. partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of all orders exist and are continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
Whitney Ck-topology
For some integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, let Jk(M,N) denote the k-jet space
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
of mappings between M and N. The jet space can be endowed with a smooth structure (i.e. a structure as a C∞ manifold) which make it into a topological space. This topology is used to define a topology on C∞(M,N).
For a fixed integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
consider an open subset and denote by Sk(U) the following:
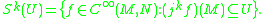
The sets Sk(U) form a basis for the Whitney Ck-topology on C∞(M,N).
Whitney C∞-topology
For each choice of , the Whitney Ck-topology gives a topology for C∞(M,N); in other words the Whitney Ck-topology tells us which subsets of C∞(M,N) are open sets. Let us denote by Wk the set of open subsets of C∞(M,N) with respect to the Whitney Ck-topology. Then the Whitney C∞-topology is defined to be the topology whose basis is given by W, where: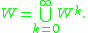
Dimensionality
Notice that C∞(M,N) has infinite dimension, whereas Jk(M,N) has finite dimension. In fact, Jk(M,N) is a real, finite dimensional manifold. To see this, let denote the space of polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, with real coefficients, in m variables and of order at most k. This is a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with dimension

Writing } then, by the standard theory of vector spaces and so is a real, finite dimensional manifold. Next, define:

Using b to denote the dimension Bkm,n, we see that , and so is a real, finite dimensional manifold.
In fact, if M and N have dimension m and n respectively then:

Topology
Consider the surjective mapping from the space of smooth maps between smooth manifolds and the k-jet space: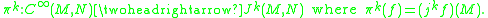
In the Whitney Ck-topology the open sets in C∞(M,N) are, by definition, the preimages of open sets in Jk(M,N). It follows that the map πk between C∞(M,N) given the Whitney Ck-topology and Jk(M,N) given the Euclidean topology is continuous.
Given the Whitney C∞-topology, the space C∞(M,N) is a Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
, i.e. every residual set is dense.

