Weil restriction
Encyclopedia
In mathematics
, restriction of scalars (also known as "Weil restriction") is a functor
which, for any finite extension
of fields L/k and any algebraic variety
X over L, produces another variety ResL/kX, defined over k. It is useful for reducing questions about varieties over large fields to questions about more complicated varieties over smaller fields.
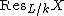from k-schemes
op to sets is defined by
(In particular, the k-rational points of
are the L-rational points of X.) The variety that represents
this functor is called the restriction of scalars, and is unique up to unique isomorphism if it exists.
From the standpoint of sheaves
of sets, restriction of scalars is just a pushforward along the morphism Spec L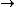
Spec k and is right adjoint to fiber product, so the above definition can be rephrased in much more generality. In particular, one can replace the extension of fields by any morphism of ringed topoi
, and the hypotheses on X can be weakened to e.g. stacks. This comes at the cost of having less control over the behavior of the restriction of scalars.
Under appropriate hypotheses (e.g., flat, proper, finitely presented), any morphism
of algebraic space
s yields a restriction of scalars functor that takes algebraic stacks to algebraic stacks, preserving properties such as Artin, Deligne-Mumford, and representability.
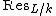(Spec L) = Spec(k) and
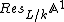
is an s-dimensional affine space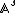
over Spec k.
2) If X is an affine L-variety, defined by
we can write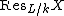
as Spec 
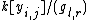, where yi,j
(
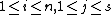) are new variables,
and gl,r are polynomials in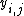
given by taking a k-basis 
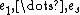of L and setting 
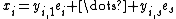and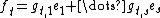 
.
3) Restriction of scalars over a finite extension of fields takes group scheme
s to group schemes.
In particular:
4) The torus
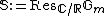
where Gm denotes the multiplicative group, plays a significant role in Hodge theory, since the Tannakian category
of real Hodge structure
s is equivalent to the category of representations of S. The real points have a Lie group
structure isomorphic to
. See Mumford–Tate group
.
5) The Weil restriction of a (commutative) group variety is again a (commutative) group variety. Aleksander Momot applied restriction of scalars on group varieties and obtained numerous generalizations of classical results from transcendence theory
.
6) Restriction of scalars on abelian varieties
(e.g. elliptic curve
s) yields abelian varieties, and Milne used this to reduce the Birch and Swinnerton-Dyer conjecture
for abelian varieties over all number fields
to the same conjecture over the rationals.
s on a commutative algebra A is not in general an A-algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, restriction of scalars (also known as "Weil restriction") is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
which, for any finite extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of fields L/k and any algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
X over L, produces another variety ResL/kX, defined over k. It is useful for reducing questions about varieties over large fields to questions about more complicated varieties over smaller fields.
Definition
Let L/k be a finite extension of fields, and X a variety defined over L. The functor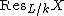 from k-schemesScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
op to sets is defined by
(In particular, the k-rational points of
are the L-rational points of X.) The variety that representsRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
this functor is called the restriction of scalars, and is unique up to unique isomorphism if it exists.
From the standpoint of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of sets, restriction of scalars is just a pushforward along the morphism Spec L
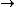Spec k and is right adjoint to fiber product, so the above definition can be rephrased in much more generality. In particular, one can replace the extension of fields by any morphism of ringed topoiTopos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, and the hypotheses on X can be weakened to e.g. stacks. This comes at the cost of having less control over the behavior of the restriction of scalars.
Properties
For any finite extension of fields, the restriction of scalars takes quasiprojective varieties to quasiprojective varieties. The dimension of the resulting variety is multiplied by the degree of the extension.Under appropriate hypotheses (e.g., flat, proper, finitely presented), any morphism
of algebraic spaceAlgebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
s yields a restriction of scalars functor that takes algebraic stacks to algebraic stacks, preserving properties such as Artin, Deligne-Mumford, and representability.
Examples and applications
1) Let L be a finite extension of k of degree s. Then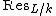(Spec L) = Spec(k) and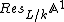is an s-dimensional affine space
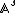over Spec k.2) If X is an affine L-variety, defined by
we can write
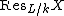as Spec 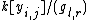, where yi,j(
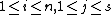) are new variables,and gl,r are polynomials in
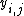given by taking a k-basis 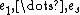of L and setting 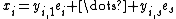and 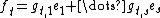.3) Restriction of scalars over a finite extension of fields takes group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s to group schemes.
In particular:
4) The torus
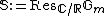
where Gm denotes the multiplicative group, plays a significant role in Hodge theory, since the Tannakian category
Tannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
of real Hodge structure
Hodge structure
In mathematics, a Hodge structure, named after W. V. D. Hodge, is an algebraic structure at the level of linear algebra, similar to the one that Hodge theory gives to the cohomology groups of a smooth and compact Kähler manifold...
s is equivalent to the category of representations of S. The real points have a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
structure isomorphic to
. See Mumford–Tate groupMumford–Tate group
In algebraic geometry, the Mumford–Tate group MT constructed from a Hodge structure F is a certain algebraic group G, named for David Mumford and John Tate. When F is given by a rational representation of an algebraic torus, the definition of G is as the Zariski closure of the image in the...
.
5) The Weil restriction of a (commutative) group variety is again a (commutative) group variety. Aleksander Momot applied restriction of scalars on group varieties and obtained numerous generalizations of classical results from transcendence theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
.
6) Restriction of scalars on abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
(e.g. elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s) yields abelian varieties, and Milne used this to reduce the Birch and Swinnerton-Dyer conjecture
Birch and Swinnerton-Dyer conjecture
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay...
for abelian varieties over all number fields
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
to the same conjecture over the rationals.
Weil restrictions vs. Greenberg transforms
Restriction of scalars is similar to the Greenberg transform, but does not generalize it, since the ring of Witt vectorWitt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s on a commutative algebra A is not in general an A-algebra.