
Watts and Strogatz model
Encyclopedia
The Watts and Strogatz model is a random graph
generation model that produces graphs with small-world properties
, including short average path length
s and high clustering
. It was proposed by Duncan J. Watts
and Steven Strogatz
in their joint 1998 Nature
paper. The model also became known as the (Watts) beta model after Watts used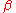 to formulate it in his popular science book Six Degrees
to formulate it in his popular science book Six Degrees
.
s dates back to the work of Paul Erdős
and Alfréd Rényi
. The graphs they considered, now known as the classical or Erdős–Rényi (ER)
graphs, offer a simple and powerful model with many applications.
However the ER
graphs do not have two important properties observed in many real-world networks:
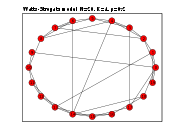
The Watts and Strogatz model was designed as the simplest possible model that addresses the first of the two limitations. It accounts for clustering while retaining the short average path lengths of the ER model. It does so by interpolating between an ER graph and a regular ring lattice
. Consequently, the model is able to at least partially explain the "small-world" phenomena in a variety of networks, such as the power grid, neural network of C. elegans
, and a network of movie actors.
 Given the desired number of nodes
Given the desired number of nodes  , the mean degree
, the mean degree
 (assumed to be an even integer), and a special parameter
(assumed to be an even integer), and a special parameter  , satisfying
, satisfying 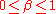 and
and 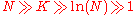 , the model constructs an undirected graph with
, the model constructs an undirected graph with  nodes and
nodes and 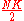 edges in the following way:
edges in the following way:
s. The algorithm introduces about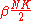 non-lattice edges. Varying
non-lattice edges. Varying 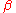 makes it possible to interpolate between a regular lattice (
makes it possible to interpolate between a regular lattice ( ) and a random graph (
) and a random graph ( ) approaching the Erdős–Rényi random graph
) approaching the Erdős–Rényi random graph
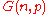 with
with  and
and 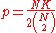 .
.
The three properties of interest are the average path length
, the clustering coefficient
, and the degree distribution
.
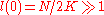 and scales linearly with the system size. In the limiting case of
and scales linearly with the system size. In the limiting case of  the graph converges to a classical random graph with
the graph converges to a classical random graph with 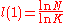 . However, in the intermediate region
. However, in the intermediate region 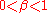 the average path length falls very rapidly with increasing
the average path length falls very rapidly with increasing 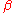 , quickly
, quickly
approaching its limiting value.
is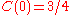 which is independent of the system size. In the limiting case of
which is independent of the system size. In the limiting case of  the clustering coefficient attains the value for classical random graphs,
the clustering coefficient attains the value for classical random graphs, 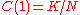 and is thus inversely proportional to the system size. In the intermediate region the clustering coefficient remains quite close to its value for the regular lattice, and only falls at relatively high
and is thus inversely proportional to the system size. In the intermediate region the clustering coefficient remains quite close to its value for the regular lattice, and only falls at relatively high 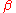 . This results in a region where the average path length falls rapidly, but the clustering coefficient does not, explaining the "small-world" phenomenon.
. This results in a region where the average path length falls rapidly, but the clustering coefficient does not, explaining the "small-world" phenomenon.
centered at . In the limiting case of
. In the limiting case of  it is Poisson distribution
it is Poisson distribution
, as with classical graphs. The degree distribution for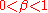 can be written as,
can be written as,
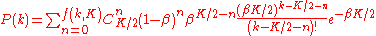
where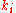 is the number of edges that the
is the number of edges that the  node has or its degree. Here
node has or its degree. Here 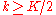 , and
, and 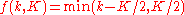 . The shape of the degree distribution is similar to that of a random graph and has a pronounced peak at
. The shape of the degree distribution is similar to that of a random graph and has a pronounced peak at 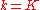 and decays exponentially for large
and decays exponentially for large 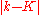 . The topology of the network is relatively homogeneous, and all nodes have more or less the same degree.
. The topology of the network is relatively homogeneous, and all nodes have more or less the same degree.
distribution. In contrast, real networks are often scale-free networks inhomogeneous in degree, having hubs and a scale-free degree distribution. Such networks are better described in that respect by the preferential attachment
family of models, such as the Barabási–Albert (BA) model
. (On the other hand, the Barabási–Albert model fails to produce the high levels of clustering seen in real networks, a shortcoming not shared by the Watts and Strogatz model. Thus, neither the Watts and Strogatz model nor the Barabási–Albert model should be viewed as fully realistic.)
The Watts and Strogatz model also implies a fixed number of nodes and thus cannot be used to model network growth.
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
generation model that produces graphs with small-world properties
Small-world network
In mathematics, physics and sociology, a small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of hops or steps...
, including short average path length
Average path length
Average path length is a concept in network topology that is defined as the average number of steps along the shortest paths for all possible pairs of network nodes...
s and high clustering
Clustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
. It was proposed by Duncan J. Watts
Duncan J. Watts
Duncan J. Watts is an Australian researcher and a principal research scientist at Yahoo! Research, where he directs the Human Social Dynamics group. He is also a past external faculty member of the Santa Fe Institute and a former professor of sociology at Columbia University, where he headed the...
and Steven Strogatz
Steven Strogatz
Steven Henry Strogatz is an American mathematician and the Jacob Gould Schurman Professor of Applied Mathematics at Cornell University...
in their joint 1998 Nature
Nature (journal)
Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...
paper. The model also became known as the (Watts) beta model after Watts used
 to formulate it in his popular science book Six Degrees
to formulate it in his popular science book Six DegreesSix Degrees: The Science of a Connected Age
Six Degrees: the science of a connected age is a popular science book by Duncan J...
.
Rationale for the model
The formal study of random graphRandom graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
s dates back to the work of Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Alfréd Rényi
Alfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
. The graphs they considered, now known as the classical or Erdős–Rényi (ER)
Erdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
graphs, offer a simple and powerful model with many applications.
However the ER
Erdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
graphs do not have two important properties observed in many real-world networks:
- They do not generate local clustering and triadic closureTriadic closureTriadic closure is a concept in social network theory, first suggested by German sociologist Georg Simmel in the early 1900s. Triadic closure is the property among 3 nodes A, B, and C, such that if a strong tie exists between A-B and A-C, there is a weak or strong tie between B-C...
s. Instead because they have a constant, random, and independent probability of two nodes being connected, ER graphs have a low clustering coefficientClustering coefficientIn graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
. - They do not account for the formation of hubs. Formally, the degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
distribution of ER graphs converges to a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, rather than a power lawPower lawA power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
observed in many real-world, scale-free networks.
The Watts and Strogatz model was designed as the simplest possible model that addresses the first of the two limitations. It accounts for clustering while retaining the short average path lengths of the ER model. It does so by interpolating between an ER graph and a regular ring lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
. Consequently, the model is able to at least partially explain the "small-world" phenomena in a variety of networks, such as the power grid, neural network of C. elegans
Caenorhabditis elegans
Caenorhabditis elegans is a free-living, transparent nematode , about 1 mm in length, which lives in temperate soil environments. Research into the molecular and developmental biology of C. elegans was begun in 1974 by Sydney Brenner and it has since been used extensively as a model...
, and a network of movie actors.
Algorithm

 , the mean degree
, the mean degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
 (assumed to be an even integer), and a special parameter
(assumed to be an even integer), and a special parameter  , satisfying
, satisfying 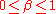 and
and 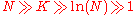 , the model constructs an undirected graph with
, the model constructs an undirected graph with  nodes and
nodes and 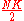 edges in the following way:
edges in the following way:- Construct a regular ring lattice, a graph with
 nodes each connected to
nodes each connected to  neighbors,
neighbors, 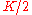 on each side. That is, if the nodes are labeled
on each side. That is, if the nodes are labeled  , there is an edge
, there is an edge 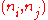 if and only if
if and only if 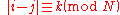 for some
for some 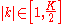
- For every node
 take every edge
take every edge 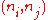 with
with  , and rewire it with probability
, and rewire it with probability 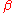 . Rewiring is done by replacing
. Rewiring is done by replacing 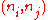 with
with 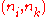 where
where  is chosen with uniform probability from all possible values that avoid loops (
is chosen with uniform probability from all possible values that avoid loops (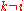 ) and link duplication (there is no edge
) and link duplication (there is no edge 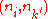 with
with  at this point in the algorithm).
at this point in the algorithm).
Properties
The underlying lattice structure of the model produces a locally clustered network, and the random links dramatically reduce the average path lengthAverage path length
Average path length is a concept in network topology that is defined as the average number of steps along the shortest paths for all possible pairs of network nodes...
s. The algorithm introduces about
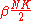 non-lattice edges. Varying
non-lattice edges. Varying 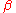 makes it possible to interpolate between a regular lattice (
makes it possible to interpolate between a regular lattice ( ) and a random graph (
) and a random graph ( ) approaching the Erdős–Rényi random graph
) approaching the Erdős–Rényi random graphErdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
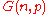 with
with  and
and 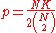 .
.The three properties of interest are the average path length
Average path length
Average path length is a concept in network topology that is defined as the average number of steps along the shortest paths for all possible pairs of network nodes...
, the clustering coefficient
Clustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
, and the degree distribution
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
.
Average path length
For a ring lattice the average path length is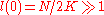 and scales linearly with the system size. In the limiting case of
and scales linearly with the system size. In the limiting case of  the graph converges to a classical random graph with
the graph converges to a classical random graph with 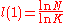 . However, in the intermediate region
. However, in the intermediate region 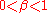 the average path length falls very rapidly with increasing
the average path length falls very rapidly with increasing 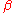 , quickly
, quicklyapproaching its limiting value.
Clustering coefficient
For the ring lattice the clustering coefficientClustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
is
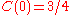 which is independent of the system size. In the limiting case of
which is independent of the system size. In the limiting case of  the clustering coefficient attains the value for classical random graphs,
the clustering coefficient attains the value for classical random graphs, 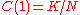 and is thus inversely proportional to the system size. In the intermediate region the clustering coefficient remains quite close to its value for the regular lattice, and only falls at relatively high
and is thus inversely proportional to the system size. In the intermediate region the clustering coefficient remains quite close to its value for the regular lattice, and only falls at relatively high 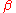 . This results in a region where the average path length falls rapidly, but the clustering coefficient does not, explaining the "small-world" phenomenon.
. This results in a region where the average path length falls rapidly, but the clustering coefficient does not, explaining the "small-world" phenomenon.- If we use the Barrat and Weigt measure for clustering
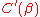 defined as the fraction between the average number of edges between the neighbors of a node and the average number of possible edges between these neighbors, or, alternatively,
defined as the fraction between the average number of edges between the neighbors of a node and the average number of possible edges between these neighbors, or, alternatively,
- then we get
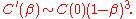
Degree distribution
The degree distribution in the case of the ring lattice is just a Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
centered at
 . In the limiting case of
. In the limiting case of  it is Poisson distribution
it is Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, as with classical graphs. The degree distribution for
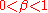 can be written as,
can be written as,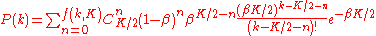
where
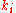 is the number of edges that the
is the number of edges that the  node has or its degree. Here
node has or its degree. Here 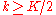 , and
, and 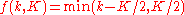 . The shape of the degree distribution is similar to that of a random graph and has a pronounced peak at
. The shape of the degree distribution is similar to that of a random graph and has a pronounced peak at 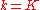 and decays exponentially for large
and decays exponentially for large 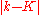 . The topology of the network is relatively homogeneous, and all nodes have more or less the same degree.
. The topology of the network is relatively homogeneous, and all nodes have more or less the same degree.Limitations
The major limitation of the model is that it produces an unrealistic degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
distribution. In contrast, real networks are often scale-free networks inhomogeneous in degree, having hubs and a scale-free degree distribution. Such networks are better described in that respect by the preferential attachment
Preferential attachment
A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who are already wealthy receive more than those who are not...
family of models, such as the Barabási–Albert (BA) model
BA model
The Barabási–Albert model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Scale-free networks are widely observed in natural and man-made systems, including the Internet, the world wide web, citation networks, and some social...
. (On the other hand, the Barabási–Albert model fails to produce the high levels of clustering seen in real networks, a shortcoming not shared by the Watts and Strogatz model. Thus, neither the Watts and Strogatz model nor the Barabási–Albert model should be viewed as fully realistic.)
The Watts and Strogatz model also implies a fixed number of nodes and thus cannot be used to model network growth.


