
Average path length
Encyclopedia
Average path length is a concept in network topology
that is defined as the average number of steps along the shortest paths for all possible pairs of network nodes
. It is a measure of the efficiency of information or mass transport on a network.
and its degree distribution
. Some examples are: the average number of clicks which will lead you from one website to another, or the number of people you will have to communicate through, on an average, to contact a complete stranger. It should not be confused with the diameter
of the network, which is defined as the maximal distance between any two nodes in the network.
The average path length distinguishes an easily negotiable network from one which is complicated and inefficient, with a shorter average path length being more desirable. However, the average path length is simply what the path length will most likely be. The network itself might have some very remotely connected nodes and many nodes which are neighbors of each other.
 with the set of vertices
with the set of vertices  . Let
. Let 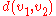 , where
, where 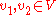 denote the shortest distance between
denote the shortest distance between 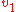 and
and 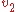 .
.
Assume that if
if  or
or 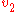 cannot be reached from
cannot be reached from 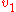 . Then, the average path length
. Then, the average path length  is:
is:
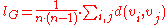
, where is the number of vertices in
is the number of vertices in  .
.
, a short average path length facilitates the quick transfer of information and reduces costs. The efficiency of mass transfer in a metabolic network
can be judged by studying its average path length. A power grid network will have less losses if its average path length is minimized.
Most real networks have a very short average path length leading to the concept of a small world
where everyone is connected to everyone else through a very short path.
As a result, most models of real networks are created with this condition in mind. One of the first models which tried to explain real networks was the random network model
. It was later followed by the Watts and Strogatz model
, and even later there were the scale-free networks starting with the BA model
. All these models had one thing in common: they all predicted very short average path length. The average path lengths of some networks are listed in Table.[1].
The average path length depends on the system size but does not change drastically with it. Small world network theory predicts that the average path length changes proportionally to log n, where n is the number of nodes in the network.
Network topology
Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....
that is defined as the average number of steps along the shortest paths for all possible pairs of network nodes
Node (networking)
In communication networks, a node is a connection point, either a redistribution point or a communication endpoint . The definition of a node depends on the network and protocol layer referred to...
. It is a measure of the efficiency of information or mass transport on a network.
Concept
Average path length is one of the three most robust measures of network topology, along with its clustering coefficientClustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
and its degree distribution
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
. Some examples are: the average number of clicks which will lead you from one website to another, or the number of people you will have to communicate through, on an average, to contact a complete stranger. It should not be confused with the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the network, which is defined as the maximal distance between any two nodes in the network.
The average path length distinguishes an easily negotiable network from one which is complicated and inefficient, with a shorter average path length being more desirable. However, the average path length is simply what the path length will most likely be. The network itself might have some very remotely connected nodes and many nodes which are neighbors of each other.
Definition
Consider an unweighed graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
 with the set of vertices
with the set of vertices  . Let
. Let 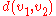 , where
, where 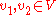 denote the shortest distance between
denote the shortest distance between 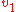 and
and 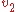 .
.Assume that
 if
if  or
or 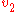 cannot be reached from
cannot be reached from 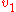 . Then, the average path length
. Then, the average path length  is:
is: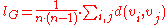
, where
 is the number of vertices in
is the number of vertices in  .
.Applications
In a real network like the World Wide WebWorld Wide Web
The World Wide Web is a system of interlinked hypertext documents accessed via the Internet...
, a short average path length facilitates the quick transfer of information and reduces costs. The efficiency of mass transfer in a metabolic network
Metabolic network modelling
Metabolic network reconstruction and simulation allows for an in depth insight into comprehending the molecular mechanisms of a particular organism, especially correlating the genome with molecular physiology...
can be judged by studying its average path length. A power grid network will have less losses if its average path length is minimized.
Most real networks have a very short average path length leading to the concept of a small world
Watts and Strogatz model
The Watts and Strogatz model is a random graph generation model that produces graphs with small-world properties, including short average path lengths and high clustering. It was proposed by Duncan J. Watts and Steven Strogatz in their joint 1998 Nature paper...
where everyone is connected to everyone else through a very short path.
As a result, most models of real networks are created with this condition in mind. One of the first models which tried to explain real networks was the random network model
Erdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
. It was later followed by the Watts and Strogatz model
Watts and Strogatz model
The Watts and Strogatz model is a random graph generation model that produces graphs with small-world properties, including short average path lengths and high clustering. It was proposed by Duncan J. Watts and Steven Strogatz in their joint 1998 Nature paper...
, and even later there were the scale-free networks starting with the BA model
BA model
The Barabási–Albert model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Scale-free networks are widely observed in natural and man-made systems, including the Internet, the world wide web, citation networks, and some social...
. All these models had one thing in common: they all predicted very short average path length. The average path lengths of some networks are listed in Table.[1].
The average path length depends on the system size but does not change drastically with it. Small world network theory predicts that the average path length changes proportionally to log n, where n is the number of nodes in the network.

