Lie conformal algebra
Encyclopedia
A Lie conformal algebra is in some sense a generalization of a Lie algebra
in the sense that it too is a "Lie algebra," though a in different pseudo-tensor category. Lie conformal algebras are very closely related to vertex algebras and have many applications in other areas of algebra and integrable systems.
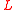in the category of vector spaces (read: 
-modules) with a morphism
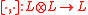
that is skew-symmetric and satisfies the Jacobi identity. A Lie conformal algebra, then, is an object
in the category of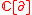 
-modules with morphism
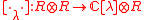
called the lambda bracket, which satisfies modified versions of bilinearity, skew-symmetry and the Jacobi identity:
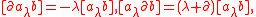
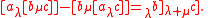
One can see that "removing all the lambda's, mu's and partials from the brackets, one simply has the definition of a Lie algebra.
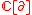it is generated by a single element 
with lambda bracket given by
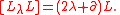
In fact, it has been shown by Wakimoto that any Lie conformal algebra with lambda bracket satisfying the Jacobi identity on one generator is actually the Virasoro conformal algebra.
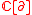-module) simple Lie conformal algebra is isomorphic to either the Virasoro conformal algebra, a current conformal algebra or a semi-direct product of the two.
There are also partial classifications of infinite subalgebras of
and 
.
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
in the sense that it too is a "Lie algebra," though a in different pseudo-tensor category. Lie conformal algebras are very closely related to vertex algebras and have many applications in other areas of algebra and integrable systems.
Definition and relation to Lie algebras
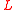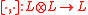
A Lie algebra is defined to be a vector space with a skew symmetric bilinear multiplication which satisfies the Jacobi identity. More generally, a Lie algebra is an object, in the category of vector spaces (read: -modules) with a morphismthat is skew-symmetric and satisfies the Jacobi identity. A Lie conformal algebra, then, is an object
in the category of 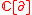-modules with morphism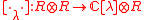called the lambda bracket, which satisfies modified versions of bilinearity, skew-symmetry and the Jacobi identity:
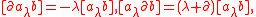
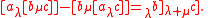
One can see that "removing all the lambda's, mu's and partials from the brackets, one simply has the definition of a Lie algebra.
Examples of Lie conformal algebras
A simple and very important example of a Lie conformal algebra is the Virasoro conformal algebra. Over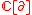 it is generated by a single element with lambda bracket given by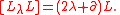In fact, it has been shown by Wakimoto that any Lie conformal algebra with lambda bracket satisfying the Jacobi identity on one generator is actually the Virasoro conformal algebra.
Classification
It has been shown that any finitely generated (as a-module) simple Lie conformal algebra is isomorphic to either the Virasoro conformal algebra, a current conformal algebra or a semi-direct product of the two.There are also partial classifications of infinite subalgebras of
and .