Van Hove singularity
Encyclopedia
A Van Hove singularity is a kink ("discontinuity") in the density of states
(DOS) of a solid
. The wavevectors at which Van Hove singularities occur are often referred to as critical points
of the Brillouin zone
. (The critical point found in phase diagram
s is a completely separate phenomenon.) The most common application of the Van Hove singularity concept comes in the analysis of optical absorption spectra. The occurrence of such singularities was first analyzed by the Belgian
physicist Léon Van Hove
in 1953 for the case of phonon
densities of states.
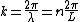
where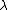
is wavelength, and n is an integer. (Positive integers will denote forward waves, negative integers will denote reverse waves.) The smallest wavelength possible is 2a which corresponds to the largest possible wave number 
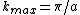and which also corresponds to the maximum possible |n|: 
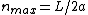. We may define the density of states g(k)dk as the number of standing waves with wave vector k to k+dk:
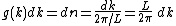
Extending the analysis to wavevectors in three dimensions the density of states in a box
will be
where
is a volume element in k-space, and which, for electrons, will need to be multiplied by a factor of 2 to account for the two possible spin
orientations. By the chain rule
, the DOS in energy space can be expressed as
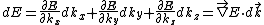
where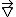
is the gradient in k-space.
The set of points in k-space which correspond to a particular energy E form a surface in k-space, and the gradient of E will be a vector perpendicular to this surface at every point. The density of states as a function of this energy E is:
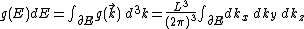
where the integral is over the surface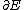
of constant E. We can choose a new coordinate system 
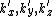such that 
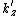is perpendicular to the surface and therefore parallel to the gradient of E. If the coordinate system is just a rotation of the original coordinate system, then the volume element in k-prime space will be
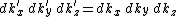
We can then write dE as:
and, substituting into the expression for g(E) we have:
where the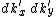
term is an area element on the constant-E surface. The clear implication of the equation for 
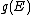is that at the 
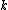-points where the dispersion relation
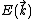has an extremum, the integrand in the DOS expression diverges. The Van Hove singularities are the features that occur in the DOS function at these 
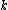-points.
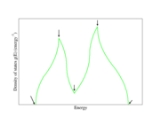
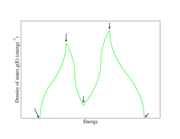
A detailed analysis shows that there are four types of Van Hove singularities in three-dimensional space, depending on whether the band structure goes through a local maximum, a local minimum or a saddle point
. In three dimensions, the DOS itself is not divergent although its derivative is. The function g(E) tends to have square-root singularities (see the Figure) since for a spherical free electron Fermi surface
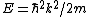so that 
.
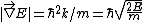In two dimensions the DOS is logarithmically divergent at a saddle point and in one dimension the DOS itself is infinite where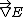
is zero.
using Fermi's Golden Rule
where the relevant matrix element
to be evaluated is the dipole operator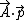
where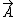 
is the vector potential
and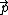
is the momentum
operator. The density of states which appears in the Fermi's Golden Rule expression is then the joint density of states, which is the number of electronic states in the conduction and valence bands that are separated by a given photon energy. The optical absorption is then essentially the product of the dipole operator matrix element (also known as the oscillator strength) and the JDOS.
The divergences in the two- and one-dimensional DOS might be expected to be a mathematical formality, but in fact they are readily observable. Highly anisotropic solids like graphite
(quasi-2D) and Bechgaard salt
s (quasi-1D) show anomalies in spectroscopic measurements that are attributable to the Van Hove singularities. Van Hove singularities play a significant role in understanding optical intensities in single-walled nanotubes
(SWNTs) which are also quasi-1D systems.
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
(DOS) of a solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
. The wavevectors at which Van Hove singularities occur are often referred to as critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. (The critical point found in phase diagram
Phase diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...
s is a completely separate phenomenon.) The most common application of the Van Hove singularity concept comes in the analysis of optical absorption spectra. The occurrence of such singularities was first analyzed by the Belgian
Belgium
Belgium , officially the Kingdom of Belgium, is a federal state in Western Europe. It is a founding member of the European Union and hosts the EU's headquarters, and those of several other major international organisations such as NATO.Belgium is also a member of, or affiliated to, many...
physicist Léon Van Hove
Léon Van Hove
Léon Van Hove was a Belgian physicist and a former Director General of CERN. He developed a scientific career spanning mathematics, solid state physics, elementary particle and nuclear physics to cosmology.-Biography:...
in 1953 for the case of phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
densities of states.
Theory
Consider a one-dimensional lattice of N particles, with each particle separated by distance a, for a total length of L = Na. A standing wave in this lattice will have a wave number k of the form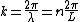where
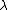is wavelength, and n is an integer. (Positive integers will denote forward waves, negative integers will denote reverse waves.) The smallest wavelength possible is 2a which corresponds to the largest possible wave number 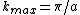and which also corresponds to the maximum possible |n|: 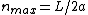. We may define the density of states g(k)dk as the number of standing waves with wave vector k to k+dk: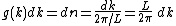Extending the analysis to wavevectors in three dimensions the density of states in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
will be
where
is a volume element in k-space, and which, for electrons, will need to be multiplied by a factor of 2 to account for the two possible spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
orientations. By the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the DOS in energy space can be expressed as
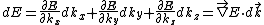
where
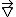is the gradient in k-space.The set of points in k-space which correspond to a particular energy E form a surface in k-space, and the gradient of E will be a vector perpendicular to this surface at every point. The density of states as a function of this energy E is:
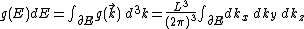
where the integral is over the surface
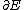of constant E. We can choose a new coordinate system 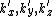such that 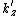is perpendicular to the surface and therefore parallel to the gradient of E. If the coordinate system is just a rotation of the original coordinate system, then the volume element in k-prime space will be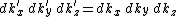We can then write dE as:
and, substituting into the expression for g(E) we have:
where the
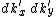term is an area element on the constant-E surface. The clear implication of the equation for 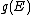is that at the 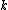-points where the dispersion relationDispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
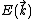has an extremum, the integrand in the DOS expression diverges. The Van Hove singularities are the features that occur in the DOS function at these 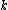-points. A detailed analysis shows that there are four types of Van Hove singularities in three-dimensional space, depending on whether the band structure goes through a local maximum, a local minimum or a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
. In three dimensions, the DOS itself is not divergent although its derivative is. The function g(E) tends to have square-root singularities (see the Figure) since for a spherical free electron Fermi surface
Fermi surface
In condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
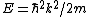so that 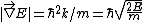.In two dimensions the DOS is logarithmically divergent at a saddle point and in one dimension the DOS itself is infinite where
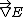is zero.Experimental observation
The optical absorption spectrum of a solid is most straightforwardly calculated from the electronic band structureElectronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
using Fermi's Golden Rule
Fermi's golden rule
In quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
where the relevant matrix element
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
to be evaluated is the dipole operator
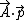where 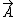is the vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
and
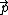is the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
operator. The density of states which appears in the Fermi's Golden Rule expression is then the joint density of states, which is the number of electronic states in the conduction and valence bands that are separated by a given photon energy. The optical absorption is then essentially the product of the dipole operator matrix element (also known as the oscillator strength) and the JDOS.
The divergences in the two- and one-dimensional DOS might be expected to be a mathematical formality, but in fact they are readily observable. Highly anisotropic solids like graphite
Graphite
The mineral graphite is one of the allotropes of carbon. It was named by Abraham Gottlob Werner in 1789 from the Ancient Greek γράφω , "to draw/write", for its use in pencils, where it is commonly called lead . Unlike diamond , graphite is an electrical conductor, a semimetal...
(quasi-2D) and Bechgaard salt
Bechgaard salt
A Bechgaard salt is any one of a number of organic charge-transfer complexes that exhibit superconductivity at low temperatures . They are named for chemist Klaus Bechgaard, who was one of the first scientists to synthesize them and demonstrate their superconductivity with the help of physicist...
s (quasi-1D) show anomalies in spectroscopic measurements that are attributable to the Van Hove singularities. Van Hove singularities play a significant role in understanding optical intensities in single-walled nanotubes
Optical properties of carbon nanotubes
Within materials science, the optical properties of carbon nanotubes refer specifically to the absorption, photoluminescence, and Raman spectroscopy of carbon nanotubes. Spectroscopic methods offer the possibility of quick and non-destructive characterization of relatively large amounts of carbon...
(SWNTs) which are also quasi-1D systems.