Twisted K-theory
Encyclopedia
In mathematics
, twisted K-theory (also called "K-theory with local coefficients") is a variation on K-theory
, a mathematical theory from the 1950s that spans algebraic topology
, abstract algebra
and operator theory
.
More specifically, twisted K-theory with twist H is a particular variant of K-theory, in which the twist is given by an integral 3-dimensional cohomology class. It is special among the various twists that K-theory admits for two reasons. First, it admits a geometric formulation. This was provided in two steps ; the first one was done in 1970 (Publ. Math. de l'IHES) by Peter Donovan and Max Karoubi http://www.numdam.org/numdam-bin/recherche?au=Karoubi,+Max&format=short; the second one in 1988 by Jonathan Rosenberg in Continuous-Trace Algebras from the Bundle Theoretic Point of View.
In physics
, it has been conjectured to classify D-branes, Ramond-Ramond field strengths
and in some cases even spinors in type II string theory
. For more information on twisted K-theory in string theory
, see K-theory (physics)
.
In the broader context of K-theory, in each subject it has numerous isomorphic formulations and, in many cases, isomorphisms relating definitions in various subjects have been proven. It also has numerous deformations, for example, in abstract algebra K-theory may be twisted by any integral cohomology class.
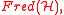
the Fredholm operator
s on Hilbert space
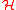, is a classifying space
for ordinary, untwisted K-theory. This means that the K-theory of the space M consists of the homotopy classes of maps
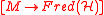
from M to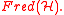
A slightly more complicated way of saying the same thing is as follows. Consider the trivial bundle of
over M, that is, the Cartesian product of M and 
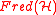. Then the K-theory of M consists of the homotopy classes of sections of this bundle.
We can make this yet more complicated by introducing a trivial
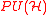
bundle
over M, where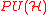 
is the group of projective unitary operators
on the Hilbert space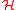
. Then the group of maps
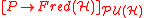
from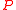
to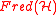 
which are equivariant
under an action of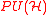
is equivalent to the original groups of maps
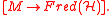
This more complicated construction of ordinary K-theory is naturally generalized to the twisted case. To see this, note that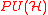
bundles on M are classified by elements H of the third integral cohomology group of M. This is a consequence of the fact that 
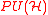topologically is a representative Eilenberg-MacLane space
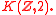
The generalization is then straightforward. Rosenberg has defined
the twisted K-theory of M with twist given by the 3-class H, to be the space of homotopy classes of sections of the trivial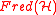
bundle over M that are covariant with respect to a 
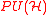bundle 
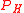fibered over M with 3-class H, that is
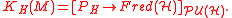
Equivalently, it is the space of homotopy classes of sections of the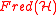
bundles associated
to a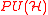
bundle with class H.
However, the direct sum of the twisted K-theories of M with all possible twists is a ring. In particular, the product of an element of K-theory with twist H with an element of K-theory with twist H' is an element of K-theory twisted by H+H'. This element can be constructed directly from the above definition by using adjoints of Fredholm operators and construct a specific 2 x 2 matrix out of them (see the reference 1, where a more natural and general Z/2-graded version is also presented). In particular twisted K-theory is a module over classical K-theory.
. The idea is that one begins with all of the even or all of the odd integral cohomology, depending on whether one wishes to calculate the twisted K0 or the twisted K1, and then one takes the cohomology with respect to a series of differential operators. The first operator, d3, for example, is the sum of the three-class H, which in string theory corresponds to the Neveu-Schwarz 3-form, and the third Steenrod square. No elementary form for the next operator, d5, has been found, although several conjectured forms exist. Higher operators do not contribute to the K-theory of a 10-manifold, which is the dimension of interest in critical superstring theory
. Over the rationals Michael Atiyah
and Graeme Segal
have shown that all of the differentials reduce to Massey product
s of H.
After taking the cohomology with respect to the full series of differentials one obtains twisted K-theory as a set, but to obtain the full group structure one in general needs to solve an extension problem.
Imagine that H is the trivial class, zero. Then d3 is also trivial. Thus its entire domain is its kernel, and nothing is in its image. Thus K0H=0(S3) is the kernel of d3 in the even cohomology, which is the full even cohomology, which consists of the integers. Similarly K1H=0(S3) consists of the odd cohomology quotiented by the image of d3, in other words quotiented by the trivial group. This leaves the original odd cohomology, which is again the integers. In conclusion, K0 and K1 of the three-sphere with trivial twist are both isomorphic to the integers. As expected, this agrees with the untwisted K-theory.
Now consider the case in which H is nontrivial. H is defined to be an element of the third integral cohomology, which is isomorphic to the integers. Thus H corresponds to a number, which we will call n. d3 now takes an element m of H0 and yields the element nm of H3. As n is not equal to zero by assumption, the only element of the kernel of d3 is the zero element, and so K0H=n(S3)=0. The image of d3 consists of all elements of the integers that are multiples of n. Therefore the odd cohomology, Z, quotiented by the image of d3, nZ, is the cyclic group of order n, Zn. In conclusion
In string theory this result reproduces the classification of D-brane
s on the 3-sphere with n units of H-flux, which corresponds to the set of symmetric boundary conditions in the supersymmetric SU(2) WZW model at level n &minus 2.
There is an extension of this calculation to the group manifold of SU(3). In this case the Steenrod square term in d3, the operator d5, and the extension problem are nontrivial.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, twisted K-theory (also called "K-theory with local coefficients") is a variation on K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, a mathematical theory from the 1950s that spans algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
.
More specifically, twisted K-theory with twist H is a particular variant of K-theory, in which the twist is given by an integral 3-dimensional cohomology class. It is special among the various twists that K-theory admits for two reasons. First, it admits a geometric formulation. This was provided in two steps ; the first one was done in 1970 (Publ. Math. de l'IHES) by Peter Donovan and Max Karoubi http://www.numdam.org/numdam-bin/recherche?au=Karoubi,+Max&format=short; the second one in 1988 by Jonathan Rosenberg in Continuous-Trace Algebras from the Bundle Theoretic Point of View.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, it has been conjectured to classify D-branes, Ramond-Ramond field strengths
Ramond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
and in some cases even spinors in type II string theory
Type II string theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges...
. For more information on twisted K-theory in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, see K-theory (physics)
K-theory (physics)
In string theory, the K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond-Ramond field strengths as well as the charges of stable D-branes....
.
In the broader context of K-theory, in each subject it has numerous isomorphic formulations and, in many cases, isomorphisms relating definitions in various subjects have been proven. It also has numerous deformations, for example, in abstract algebra K-theory may be twisted by any integral cohomology class.
The definition
To motivate Rosenberg's geometric formulation of twisted K-theory, start from the Atiyah-Jänich theorem, stating that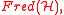the Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
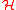, is a classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for ordinary, untwisted K-theory. This means that the K-theory of the space M consists of the homotopy classes of maps
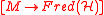
from M to
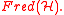
A slightly more complicated way of saying the same thing is as follows. Consider the trivial bundle of
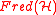over M, that is, the Cartesian product of M and . Then the K-theory of M consists of the homotopy classes of sections of this bundle.We can make this yet more complicated by introducing a trivial
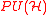
bundle
over M, where 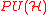is the group of projective unitary operatorsProjective unitary group
In mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
on the Hilbert space
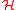. Then the group of maps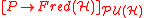from
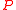to 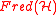which are equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
under an action of
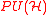is equivalent to the original groups of maps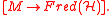This more complicated construction of ordinary K-theory is naturally generalized to the twisted case. To see this, note that
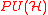bundles on M are classified by elements H of the third integral cohomology group of M. This is a consequence of the fact that 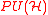topologically is a representative Eilenberg-MacLane spaceEilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
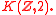
The generalization is then straightforward. Rosenberg has defined
- KH(M),
the twisted K-theory of M with twist given by the 3-class H, to be the space of homotopy classes of sections of the trivial
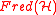bundle over M that are covariant with respect to a 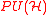bundle 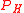fibered over M with 3-class H, that is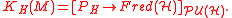Equivalently, it is the space of homotopy classes of sections of the
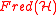bundles associatedAssociated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
to a
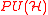bundle with class H.What is it?
When H is the trivial class, twisted K-theory is just untwisted K-theory, which is a ring. However when H is nontrivial this theory is no longer a ring. It has an addition, but it is no longer closed under multiplication.However, the direct sum of the twisted K-theories of M with all possible twists is a ring. In particular, the product of an element of K-theory with twist H with an element of K-theory with twist H' is an element of K-theory twisted by H+H'. This element can be constructed directly from the above definition by using adjoints of Fredholm operators and construct a specific 2 x 2 matrix out of them (see the reference 1, where a more natural and general Z/2-graded version is also presented). In particular twisted K-theory is a module over classical K-theory.
How to calculate it
Physicist typically want to calculate twisted K-theory using the Atiyah-Hirzebruch spectral sequenceAtiyah-Hirzebruch spectral sequence
In mathematics, the Atiyah–Hirzebruch spectral sequence is a spectral sequence for calculating generalized cohomology, introduced by in the special case of K-theory. For a CW complex X, it relates the generalized cohomology groups...
. The idea is that one begins with all of the even or all of the odd integral cohomology, depending on whether one wishes to calculate the twisted K0 or the twisted K1, and then one takes the cohomology with respect to a series of differential operators. The first operator, d3, for example, is the sum of the three-class H, which in string theory corresponds to the Neveu-Schwarz 3-form, and the third Steenrod square. No elementary form for the next operator, d5, has been found, although several conjectured forms exist. Higher operators do not contribute to the K-theory of a 10-manifold, which is the dimension of interest in critical superstring theory
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
. Over the rationals Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and Graeme Segal
Graeme Segal
Graeme Bryce Segal is a British mathematician, and professor at the University of Oxford.Segal was educated at the University of Sydney, where he received his BSc degree in 1961. He went on to receive his D.Phil...
have shown that all of the differentials reduce to Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s of H.
After taking the cohomology with respect to the full series of differentials one obtains twisted K-theory as a set, but to obtain the full group structure one in general needs to solve an extension problem.
Example: the three-sphere
The three-sphere, S3, has trivial cohomology except for H0(S3) and H3(S3) which are both isomorphic to the integers. Thus the even and odd cohomologies are both isomorphic to the integers. Because the three-sphere is of dimension three, which is less than five, the third Steenrod square is trivial on its cohomology and so the first nontrivial differential is just d3 = H. The later differentials increase the degree of a cohomology class by more than three and so are again trivial; thus the twisted K-theory is just the cohomology of the operator d3 which acts on a class by cupping it with the 3-class H.Imagine that H is the trivial class, zero. Then d3 is also trivial. Thus its entire domain is its kernel, and nothing is in its image. Thus K0H=0(S3) is the kernel of d3 in the even cohomology, which is the full even cohomology, which consists of the integers. Similarly K1H=0(S3) consists of the odd cohomology quotiented by the image of d3, in other words quotiented by the trivial group. This leaves the original odd cohomology, which is again the integers. In conclusion, K0 and K1 of the three-sphere with trivial twist are both isomorphic to the integers. As expected, this agrees with the untwisted K-theory.
Now consider the case in which H is nontrivial. H is defined to be an element of the third integral cohomology, which is isomorphic to the integers. Thus H corresponds to a number, which we will call n. d3 now takes an element m of H0 and yields the element nm of H3. As n is not equal to zero by assumption, the only element of the kernel of d3 is the zero element, and so K0H=n(S3)=0. The image of d3 consists of all elements of the integers that are multiples of n. Therefore the odd cohomology, Z, quotiented by the image of d3, nZ, is the cyclic group of order n, Zn. In conclusion
- K1H=n(S3) = Zn.
In string theory this result reproduces the classification of D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
s on the 3-sphere with n units of H-flux, which corresponds to the set of symmetric boundary conditions in the supersymmetric SU(2) WZW model at level n &minus 2.
There is an extension of this calculation to the group manifold of SU(3). In this case the Steenrod square term in d3, the operator d5, and the extension problem are nontrivial.