
Massey product
Encyclopedia

Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Massey product is a cohomology operation
Cohomology operation
In mathematics, the cohomology operation concept became central to algebraic topology, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor defining a cohomology theory, then a cohomology operation should be a natural transformation from...
of higher order introduced in , which generalizes the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
.
Massey triple product
The Massey product is defined algebraically at the level of chains (at the level of a differential graded algebraDifferential graded algebra
In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.- Definition :...
, or DGA); the Massey product of elements of cohomology is obtained by lifting the elements to equivalence classes of chains, taking the Massey products of these, and then pushing down to cohomology. This may result in a well-defined cohomology class, or may result in indeterminacy.
In a DGA Γ with differential d, the cohomology
H(Γ) is an algebra. Define
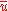 to be (-1)deg(u)+1u. The cohomology class of an element u of Γ will be denoted by
to be (-1)deg(u)+1u. The cohomology class of an element u of Γ will be denoted by 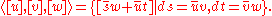
The Massey product of 3 cohomology classes is not an element of H(Γ) but a set of elements of H(Γ), possibly empty and possibly containing more than one element. If
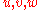 have degrees
have degrees  then the Massey product has degree
then the Massey product has degree  with the −1 coming from the differential d.
with the −1 coming from the differential d.The Massey product is nonempty if the products uv and vw are both exact, in which case
all its elements are in the same element of the quotient group
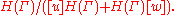
So the Massey product can be regarded as a function defined on triples of classes such that the product of the first or last two is zero, taking values in the above quotient group.
More casually, if the two pairwise products
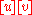 and
and 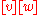 both vanish in homology (
both vanish in homology ( ), i.e.
), i.e.  and
and  for some chains
for some chains  and
and  , then the triple product
, then the triple product  vanishes "for two different reasons" – it is the boundary of
vanishes "for two different reasons" – it is the boundary of  and
and 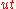 (since
(since 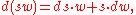 and
and 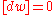 because elements of homology are cycles). The bounding chains
because elements of homology are cycles). The bounding chains  and
and  have indeterminacy, which disappears when one moves to homology, and since
have indeterminacy, which disappears when one moves to homology, and since  and
and 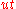 have the same boundary, subtracting them (the sign convention is to correctly handle the grading) gives a cocycle (the boundary of the difference vanishes), and one thus obtains a well-defined element of cohomology – this step is analogous to defining the n+1st homotopy or homology group in terms of indeterminacy in null-homotopies/null-homologies of n-dimensional maps/chains.
have the same boundary, subtracting them (the sign convention is to correctly handle the grading) gives a cocycle (the boundary of the difference vanishes), and one thus obtains a well-defined element of cohomology – this step is analogous to defining the n+1st homotopy or homology group in terms of indeterminacy in null-homotopies/null-homologies of n-dimensional maps/chains.Geometrically, in singular cohomology of a manifold, one can interpret the product dually in terms of bounding manifolds and intersections, following Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
: dual to cocycles are cycles, often representable as closed manifolds (without boundary), dual to product is intersection, and dual to the subtraction of the bounding products is gluing the two bounding manifolds together along the boundary, obtaining a closed manifold which represents the homology class dual of the Massey product. In reality homology classes of manifolds cannot always be represented by manifolds – a representing cycle may have singularities – but with this caveat the dual picture is correct.
Higher order Massey products
More generally the n-fold Massey product ⟨a1,1, a2,2, ...,an,n⟩ of n elements of H(Γ) is defined to be the set of elements of the form
for all solutions of the equations
 , 1 ≤ i ≤ j ≤ n, (i,j) ≠ (1,n).
, 1 ≤ i ≤ j ≤ n, (i,j) ≠ (1,n).In other words it can be thought of as the obstruction to solving the latter equations for all 1≤i≤j≤n, in the sense that it contains the 0 cohomology class if and only if these equations are solvable.
This n-fold Massey product is an n−1 order cohomology operation, meaning that for it to be nonempty many lower order Massey operations have to contain 0, and moreover the cohomology classes it represents all differ by terms involving lower order operations. The 2-fold Massey product is just the usual cup product and is a first order cohomology operation, and the 3-fold Massey product is the same as the triple Massey product defined above and is a secondary cohomology operation.
described a further generalization called Matric Massey products, which can be used to describe the differentials of the Eilenberg–Moore spectral sequence.
Applications

Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
gives an example where the triple Massey product is defined and non-zero.
If u, v, and w are 1-cochains dual to the 3 rings, then the product of any two is a multiple of the corresponding linking number
Linking number
In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
and is therefore zero, while the Massey product of all three elements is non-zero, showing that the Borromean rings are linked. The algebra reflects the geometry: the rings are pairwise unlinked, corresponding to the pairwise (2-fold) products vanishing, but are overall linked, corresponding to the 3-fold product not vanishing.
More generally, n-component Brunnian links – links such that any (n − 1)-component sublink is unlinked, but the overall n-component link is non-trivially linked – correspond to n-fold Massey products, with the unlinking of the (n − 1)-component sublink corresponding to the vanishing of the (n − 1)-fold Massey products, and the overall n-component linking corresponding to the non-vanishing of the n-fold Massey product.
used the Massey triple product to prove that the Whitehead product
Whitehead product
In mathematics, the Whitehead product is a graded quasi-Lie algebra structure on the homotopy groups of a space. It was defined by J. H. C. Whitehead in .- Definition :Given elements f \in \pi_k, g \in \pi_l, the Whitehead bracket...
satisfies the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.
Massey products of higher order appear in the Atiyah–Hirzebruch spectral sequence (AHSS), which computes twisted K-theory
Twisted K-theory
In mathematics, twisted K-theory is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory....
with twist given by a 3-class H. showed that rationally the higher order differentials

in the AHSS acting on a class x are given by the Massey product of p copies of H with a single copy of x.
A manifold on which all Massey products vanish is a formal manifold
Formal manifold
In geometry and topology, a formal manifold can mean one of a number of related concepts:* In the sense of Dennis Sullivan, a formal manifold is one whose real homotopy type is a formal consequence of its real cohomology ring; algebro-topologically this means that all Massey products vanish.* A...
: its real homotopy type follows ("formally") from its real cohomology ring.
showed Kähler manifolds are formal.
use a Massey product to show that the homotopy type of the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of two points in a lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
depends non-trivially on the simple homotopy type of the lens space.

