In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

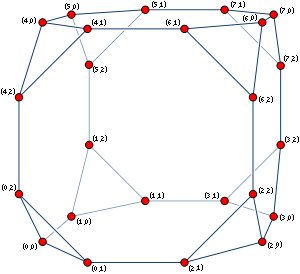
, the cube-connected cycles is an undirected cubic graph

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

, formed by replacing each vertex

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 of a hypercube graph by a cycle

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

. It was introduced by for use as a network topology

Network topology

Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....

 in parallel computing

Parallel computing

Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...

.

Definition

The cube-connected cycles of order n (denoted CCC_n) can be defined as a graph formed from a set of n2ⁿ nodes, indexed by pairs of numbers (x, y) where 0 ≤ x < 2ⁿ and 0 ≤ y < n. Each such node is connected to three neighbors: , , and , where "⊕" denotes the bitwise

Bitwise operation

A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...

 exclusive or operation on binary numbers.

Properties

The cube-connected cycles of order n is the Cayley graph

Cayley graph

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...

 of a
group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 that acts

Group action

In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...

 on binary words of length n by rotation

Circular shift

In combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation...

 and flipping bits of the word . The generators used to form this Cayley graph from the group are the group elements that act by rotating the word one position left, rotating it one position right, or flipping its first bit. Because it is a Cayley graph, it is vertex-transitive

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

: there is a symmetry of the graph mapping any vertex to any other vertex.

The diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

 of the cube-connected cycles of order n is for any n ≥ 4; the farthest point from (x, y) is (2ⁿ − x − 1, (y + n/2) mod n) . showed that the crossing number

Crossing number (graph theory)

In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...

 of CCC_n is ((1/20) + o(1)) 4ⁿ.

According to the Lovász conjecture

Lovász conjecture

In graph theory, the Lovász conjecture is a classical problem on Hamiltonian paths in graphs. It says:The original article of Lovász stated the result in the opposite, butthis version became standard...

, the cube-connected cycle graph should always contain a Hamiltonian cycle, and this is now known to be true. More generally, although these graphs are not pancyclic

Pancyclic graph

In the mathematical study of graph theory, a pancyclic graph is a directed or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph...

, they contain cycles of all but a finite number of possible even lengths, and when n is odd they also contain many of the possible odd lengths of cycles .

Parallel processing application

Cube-connected cycles were investigated by , who applied these graphs as the interconnection pattern

Network topology

Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....

 of a network connecting the processors in a parallel computer

Parallel computing

Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...

. In this application, cube-connected cycles have the connectivity advantages of hypercubes while only requiring three connections per processor. Preparata and Vuillemin showed that a planar layout based on this network has optimal area × time² complexity for many parallel processing tasks.