True arithmetic
Encyclopedia
In mathematical logic
, true arithmetic is the theory
Th(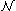
) of the natural number
s in the language of first-order Peano arithmetic (Boolos, Burgess, and Jeffrey 2002:295). Tarski's indefinability theorem
shows that this theory is not arithmetically definable.
. The language of first-order arithmetic consists of all the well-formed formulas in this signature.
The structure
is a model of Peano arithmetic defined as follows:
This structure is known as the standard model or intended interpretation
of first-order arithmetic.
A sentence
in the language of first-order arithmetic is said to be true in
if it is true in the structure just defined. The notation 
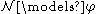is used to indicate that the sentence φ is true in 
True arithmetic is the set of all sentences in the language of first-order arithmetic that are true in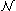
. This set is, equivalently, the (complete) theory of the structure 
(see theories associated with a structure).
of Alfred Tarski
(1936). It states that
the set is not arithmetically definable. This means that there is no "universal formula" φ in the signature of first-order arithmetic such that, for every sentence θ in this signature,
if and only if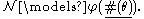 
Here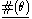
is the numeral of the canonical Gödel number
of the sentence θ.
Post's theorem
is a sharper version of the indefinability theorem that shows a relationship between the definability of and the Turing degree
s, using the arithmetical hierarchy
. For each natural number n, let be the subset of consisting of only sentences that are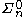
or lower in the arithmetical hierarchy. Post's theorem shows that, for each n, is arithmetically definable, but only by a formula of complexity higher than 
. Thus no single formula can define , because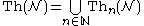
but no single formula can define for arbitrarily large n.
of is 0ω, and so is not decidable nor recursively enumerable
.
is closely related to the theory of the recursively enumerable Turing degrees, in the signature of partial orders (Shore 1999:184). In particular, there are computable functions S and T such that:
, and so has
models for each uncountable cardinal 
. As there are continuum many types over the empty set, true arithmetic also has 
countable models. Since the theory is complete
, all of its models are elementarily equivalent.
that are satisfied by the standard model of second-order arithmetic, whose first-order part is the structure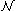
and whose second-order part consists of every subset of 
.
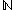The true theory of first-order arithmetic, , is a subset of the true theory of second order arithmetic, and is definable in second-order arithmetic. However, the generalization of Post's theorem to the analytical hierarchy
shows that the true theory of second-order arithmetic is not definable by any single formula in second-order arithmetic.
Simpson (1977) has shown that the true theory of second-order arithmetic is computably interpretable with the theory of the partial order of all Turing degree
s, in the signature of partial orders, and vice versa.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, true arithmetic is the theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
Th(
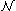) of the natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s in the language of first-order Peano arithmetic (Boolos, Burgess, and Jeffrey 2002:295). Tarski's indefinability theorem
Tarski's indefinability theorem
Tarski's undefinability theorem, stated and proved by Alfred Tarski in 1936, is an important limitative result in mathematical logic, the foundations of mathematics, and in formal semantics...
shows that this theory is not arithmetically definable.
Definition
The signature of Peano arithmetic includes the addition, multiplication, and successor function symbols, the equality and less-than relation symbols, and a constant symbol for 0. The (well-formed) formulas in this signature are built up in the usual manner of first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. The language of first-order arithmetic consists of all the well-formed formulas in this signature.
The structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
is a model of Peano arithmetic defined as follows:
- The domain of discourseDomain of discourseIn the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
is the set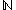
of natural numbers. - The symbol 0 is interpreted as the number 0.
- The function symbols are interpreted as the usual arithmetical operations on
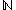
- The equality and less-than relation symbols are interpreted as the usual equality and order relation on
This structure is known as the standard model or intended interpretation
Intended interpretation
One who constructs a syntactical system usually has in mind from the outset some interpretation of this system. While this intended interpretation can have no explicit indication in the syntactical rules - since these rules must be strictly formal - the author's intention respecting...
of first-order arithmetic.
A sentence
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
in the language of first-order arithmetic is said to be true in
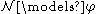if it is true in the structure just defined. The notation is used to indicate that the sentence φ is true in True arithmetic is the set of all sentences in the language of first-order arithmetic that are true in
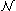. This set is, equivalently, the (complete) theory of the structure (see theories associated with a structure).Arithmetic indefinability
The central result on true arithmetic is the indefinability theoremTarski's indefinability theorem
Tarski's undefinability theorem, stated and proved by Alfred Tarski in 1936, is an important limitative result in mathematical logic, the foundations of mathematics, and in formal semantics...
of Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
(1936). It states that
the set is not arithmetically definable. This means that there is no "universal formula" φ in the signature of first-order arithmetic such that, for every sentence θ in this signature,
if and only if 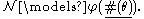Here
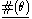is the numeral of the canonical Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
of the sentence θ.
Post's theorem
Post's theorem
In computability theory Post's theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees.- Background :The statement of Post's theorem uses several concepts relating to definability and recursion theory...
is a sharper version of the indefinability theorem that shows a relationship between the definability of and the Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
s, using the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
. For each natural number n, let be the subset of consisting of only sentences that are
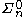or lower in the arithmetical hierarchy. Post's theorem shows that, for each n, is arithmetically definable, but only by a formula of complexity higher than . Thus no single formula can define , because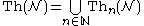but no single formula can define for arbitrarily large n.
Computability properties
As discussed above, is not arithmetically definable, by Tarski's theorem. A corollary of Post's theorem establishes that the Turing degreeTuring degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
of is 0ω, and so is not decidable nor recursively enumerable
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
.
is closely related to the theory of the recursively enumerable Turing degrees, in the signature of partial orders (Shore 1999:184). In particular, there are computable functions S and T such that:
- For each sentence φ in the signature of first order arithmetic, φ is in if and only if S(φ) is in
- For each sentence ψ in the signature of partial orders, ψ is in if and only if T(ψ) is in .
Model-theoretic properties
True arithmetic is an unstable theoryStable theory
In model theory, a complete theory is called stable if it does not have too many types. One goal of classification theory is to divide all complete theories into those whose models can be classified and those whose models are too complicated to classify, and to classify all models in the cases...
, and so has
models for each uncountable cardinal . As there are continuum many types over the empty set, true arithmetic also has countable models. Since the theory is completeComplete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
, all of its models are elementarily equivalent.
True theory of second-order arithmetic
The true theory of second-order arithmetic consists of all the sentences in the language of second-order arithmeticSecond-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
that are satisfied by the standard model of second-order arithmetic, whose first-order part is the structure
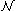and whose second-order part consists of every subset of 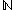.The true theory of first-order arithmetic, , is a subset of the true theory of second order arithmetic, and is definable in second-order arithmetic. However, the generalization of Post's theorem to the analytical hierarchy
Analytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
shows that the true theory of second-order arithmetic is not definable by any single formula in second-order arithmetic.
Simpson (1977) has shown that the true theory of second-order arithmetic is computably interpretable with the theory of the partial order of all Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
s, in the signature of partial orders, and vice versa.