Intended interpretation
Encyclopedia
One who constructs a syntactical system
usually has in mind from the outset some interpretation
of this system. While this intended interpretation (called standard model in mathematical logic
—a term introduced by Abraham Robinson
in 1960) can have no explicit indication in the syntactical rules
- since these rules must be strictly formal - the author's intention respecting interpretation naturally affects his choice of the formation
and transformation rules of the syntactical system. For example, he chooses primitive signs
in such a way that certain concepts can be expressed; he chooses sentential formulas in such a way that their counterparts in the intended interpretation can appear as meaningful
declarative sentences; his choice of primitive sentences
must meet the requirement that these primitive sentences come out as true
sentences
in the interpretation; his rules of inference must be such that if by one of these rules the sentence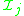
is directly derivable
from a sentence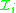
, then 
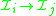turns out to be a true sentence (under the customary interpretation of as meaning implication
). These requirements ensure that all provable
sentences also come out to be true.
Most formal systems have many more models than they were intended to have (the existence of non-standard model
s is an example). When we speak about 'models' in empirical sciences, we mean, if we want reality
to be a model of our science, to speak about an intended model. A model in the empirical sciences is an intended factually-true descriptive interpretation (or in other contexts: a non-intended arbitrary interpretation used to clarify such an intended factually-true descriptive interpretation.) All models are interpretations that have the same domain of discourse
as the intended one, but other assignments for non-logical constants.
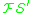) whose alphabet α consists only of three symbols { 
, 
, 
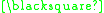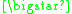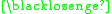} and whose formation rule for formulas is:
The single axiom schema
of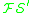
is:
A formal proof can be constructed as follows: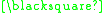
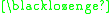
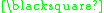
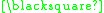
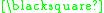
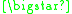
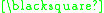
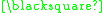
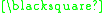
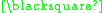
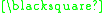
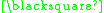
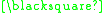
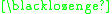
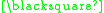
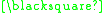
In this example the theorem produced "
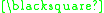
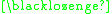
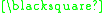
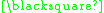" can be interpreted as meaning "One plus three equals four." A different interpretation would be to read it backwards as "Four minus three equals one."
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
usually has in mind from the outset some interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
of this system. While this intended interpretation (called standard model in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
—a term introduced by Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
in 1960) can have no explicit indication in the syntactical rules
Deductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
- since these rules must be strictly formal - the author's intention respecting interpretation naturally affects his choice of the formation
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
and transformation rules of the syntactical system. For example, he chooses primitive signs
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
in such a way that certain concepts can be expressed; he chooses sentential formulas in such a way that their counterparts in the intended interpretation can appear as meaningful
Meaning (linguistics)
In linguistics, meaning is what is expressed by the writer or speaker, and what is conveyed to the reader or listener, provided that they talk about the same thing . In other words if the object and the name of the object and the concepts in their head are the same...
declarative sentences; his choice of primitive sentences
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
must meet the requirement that these primitive sentences come out as true
True
True may refer to:* Truth, the state of being in accord with fact or reality-Music:* True , 1996* True , 2002* True , 1983** "True"...
sentences
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
in the interpretation; his rules of inference must be such that if by one of these rules the sentence
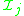is directly derivableFormal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
from a sentence
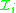, then 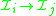turns out to be a true sentence (under the customary interpretation of as meaning implicationMaterial conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
). These requirements ensure that all provable
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
sentences also come out to be true.
Most formal systems have many more models than they were intended to have (the existence of non-standard model
Non-standard model
In model theory, a discipline within mathematical logic, a non-standard model is a model of a theory that is not isomorphic to the intended model . If the intended model is infinite and the language is first-order, then the Löwenheim-Skolem theorems guarantee the existence of non-standard models...
s is an example). When we speak about 'models' in empirical sciences, we mean, if we want reality
Reality
In philosophy, reality is the state of things as they actually exist, rather than as they may appear or might be imagined. In a wider definition, reality includes everything that is and has been, whether or not it is observable or comprehensible...
to be a model of our science, to speak about an intended model. A model in the empirical sciences is an intended factually-true descriptive interpretation (or in other contexts: a non-intended arbitrary interpretation used to clarify such an intended factually-true descriptive interpretation.) All models are interpretations that have the same domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
as the intended one, but other assignments for non-logical constants.
Example
Given a simple formal system (we shall call this one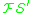) whose alphabet α consists only of three symbols { 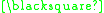, , 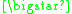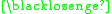} and whose formation rule for formulas is:
- 'Any string of symbols of
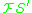which is at least 6 symbols long, and which is not infinitely long, is a formula of 
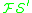. Nothing else is a formula of 
.'
The single axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of
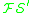is:- "
* 
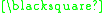
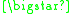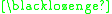
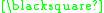* " (where " * " is a metasyntactic variableMetasyntactic variableIn computer science, programmers use metasyntactic variables to describe a placeholder name or an alias term commonly used to denote the subject matter under discussion or an arbitrary member of a class of things under discussion...
standing for a finite string of "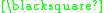
"s )
A formal proof can be constructed as follows:
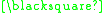
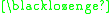
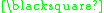
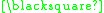
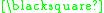
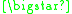
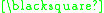
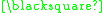
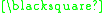
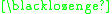
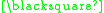
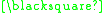
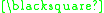
In this example the theorem produced "
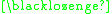
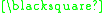
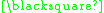" can be interpreted as meaning "One plus three equals four." A different interpretation would be to read it backwards as "Four minus three equals one."