
Sylvester's sequence
Encyclopedia
In number theory
, Sylvester's sequence is an integer sequence
in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:
Sylvester's sequence is named after James Joseph Sylvester
, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series
of unit fraction
s that converges to 1 more rapidly than any other series of unit fractions with the same sum. The recurrence
by which it is defined allows the numbers in the sequence to be factored
more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its members. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian
Einstein manifold
s, and hard instances for online algorithm
s.

The product of an empty set
is 1, so s0 = 2.
Alternatively, one may define the sequence by the recurrence
 with s0 = 2.
with s0 = 2.
It is straightforward to show by induction that this is equivalent to the other definition.

for a number E that is approximately 1.264. This formula has the effect of the following algorithm
:
This would only be a practical algorithm if we had a better way of calculating E to the requisite number of places than calculating sn and taking its repeated square root.
The double-exponential growth of the Sylvester sequence is unsurprising if one compares it to the sequence of Fermat numbers Fn; the Fermat numbers are usually defined by a doubly exponential formula,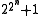 , but they can also be defined by a product formula very similar to that defining Sylvester's sequence:
, but they can also be defined by a product formula very similar to that defining Sylvester's sequence:
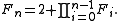
s formed by the reciprocals
of the values in Sylvester's sequence generate an infinite series
: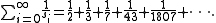
The partial sums of this series have a simple form,
This may be proved by induction, or more directly by noting that the recursion implies that
so the sum telescopes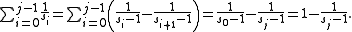
Since this sequence of partial sums (sj-2)/(sj-1) converges to one, the overall series forms an infinite Egyptian fraction representation of the number one:
One can find finite Egyptian fraction representations of one, of any length, by truncating this series and subtracting one from the last denominator: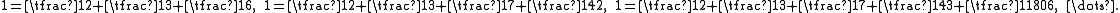
The sum of the first k terms of the infinite series provides the closest possible underestimate of 1 by any k-term Egyptian fraction. For example, the first four terms add to 1805/1806, and therefore any Egyptian fraction for a number in the open interval (1805/1806,1) requires at least five terms.
It is possible to interpret the Sylvester sequence as the result of a greedy algorithm for Egyptian fractions
, that at each step chooses the smallest possible denominator that makes the partial sum of the series be less than one. Alternatively, the terms of the sequence after the first can be viewed as the denominators of the odd greedy expansion of 1/2.
To make this more precise, it follows from results of that, if a sequence of integers grows quickly enough that
grows quickly enough that
and if the series
converges to a rational number A, then, for all n after some point, this sequence must be defined by the same recurrence
that can be used to define Sylvester's sequence.
conjectured
that, in results of this type, the inequality bounding the growth of the sequence could be replaced by a weaker condition,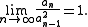
surveys progress related to this conjecture; see also .
s, as any prime can divide at most one number in the sequence. More strongly, no prime factor of a number in the sequence can be congruent to 5 (mod 6), and the sequence can be used to prove that there are infinitely many primes congruent to 7 (mod 12) .
Some effort has been expended in an attempt to factor the numbers in Sylvester's sequence, but much remains unknown about their factorization. For instance, it is not known if all numbers in the sequence are squarefree
, although all the known terms are.
As describes, it is easy to determine which Sylvester number (if any) a given prime p divides: simply compute the recurrence defining the numbers modulo p until finding either a number that is congruent to zero (mod p) or finding a repeated modulus. Via this technique he found that 1166 out of the first three million primes are divisors of Sylvester numbers, and that none of these primes has a square that divides a Sylvester number. A general result of implies that the set of prime factors of Sylvester numbers has density zero in the set of all primes.
The following table shows known factorizations of these numbers, (except the first four, which are all prime):
As is customary, Pn and Cn denote prime and composite numbers n digits long.
Einstein manifold
s having the differential topology
of odd-dimensional spheres
or exotic sphere
s. They show that the number of distinct Sasakian Einstein metrics on a topological sphere of dimension 2n − 1 is at least proportional to sn and hence has double exponential growth with n.
As describe, and used values derived from Sylvester's sequence to construct lower bound examples for online
bin packing algorithm
s. similarly use the sequence to lower bound the performance of a two-dimensional cutting stock algorithm.
Znám's problem
concerns sets of numbers such that each number in the set divides but is not equal to the product of all the other numbers, plus one. Without the inequality requirement, the values in Sylvester's sequence would solve the problem; with that requirement, it has other solutions derived from recurrences similar to the one defining Sylvester's sequence. Solutions to Znám's problem have applications to the classification of surface singularities (Brenton and Hill 1988) and to the theory of nondeterministic finite automata.
describes an application of the closest approximations to one by k-term sums of unit fractions, in lower-bounding the number of divisors of any perfect number
, and uses the same property to lower bound the size of certain groups
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Sylvester's sequence is an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:
- 2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 .
Sylvester's sequence is named after James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s that converges to 1 more rapidly than any other series of unit fractions with the same sum. The recurrence
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
by which it is defined allows the numbers in the sequence to be factored
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its members. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian
Sasakian manifold
In differential geometry, a Sasakian manifold is a contact manifold equipped with a special kind of Riemannian metric g, called a Sasakian metric.-Definition:...
Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
s, and hard instances for online algorithm
Online algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
s.
Formal definitions
Formally, Sylvester's sequence can be defined by the formula
The product of an empty set
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
is 1, so s0 = 2.
Alternatively, one may define the sequence by the recurrence
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
 with s0 = 2.
with s0 = 2.It is straightforward to show by induction that this is equivalent to the other definition.
Closed form formula and asymptotics
The Sylvester numbers grow doubly exponentially as a function of n. Specifically, it can be shown that
for a number E that is approximately 1.264. This formula has the effect of the following algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
:
- s0 is the nearest integer to E2; s1 is the nearest integer to E4; s2 is the nearest integer to E8; for sn, take E2, square it n more times, and take the nearest integer.
This would only be a practical algorithm if we had a better way of calculating E to the requisite number of places than calculating sn and taking its repeated square root.
The double-exponential growth of the Sylvester sequence is unsurprising if one compares it to the sequence of Fermat numbers Fn; the Fermat numbers are usually defined by a doubly exponential formula,
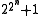 , but they can also be defined by a product formula very similar to that defining Sylvester's sequence:
, but they can also be defined by a product formula very similar to that defining Sylvester's sequence: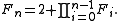
Connection with Egyptian fractions
The unit fractionUnit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s formed by the reciprocals
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the values in Sylvester's sequence generate an infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
:
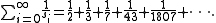
The partial sums of this series have a simple form,

This may be proved by induction, or more directly by noting that the recursion implies that

so the sum telescopes
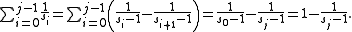
Since this sequence of partial sums (sj-2)/(sj-1) converges to one, the overall series forms an infinite Egyptian fraction representation of the number one:

One can find finite Egyptian fraction representations of one, of any length, by truncating this series and subtracting one from the last denominator:
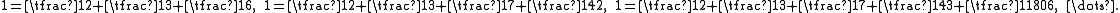
The sum of the first k terms of the infinite series provides the closest possible underestimate of 1 by any k-term Egyptian fraction. For example, the first four terms add to 1805/1806, and therefore any Egyptian fraction for a number in the open interval (1805/1806,1) requires at least five terms.
It is possible to interpret the Sylvester sequence as the result of a greedy algorithm for Egyptian fractions
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
, that at each step chooses the smallest possible denominator that makes the partial sum of the series be less than one. Alternatively, the terms of the sequence after the first can be viewed as the denominators of the odd greedy expansion of 1/2.
Uniqueness of quickly growing series with rational sums
As Sylvester himself observed, Sylvester's sequence seems to be unique in having such quickly growing values, while simultaneously having a series of reciprocals that converges to a rational number.To make this more precise, it follows from results of that, if a sequence of integers
 grows quickly enough that
grows quickly enough that
and if the series

converges to a rational number A, then, for all n after some point, this sequence must be defined by the same recurrence

that can be used to define Sylvester's sequence.
conjectured
Erdos conjecture
The prolific mathematician Paul Erdős and his various collaborators made many famous mathematical conjectures, over a wide field of subjects.Some of these are the following:* The Cameron–Erdős conjecture on sum-free sets of integers, proved by Ben Green....
that, in results of this type, the inequality bounding the growth of the sequence could be replaced by a weaker condition,
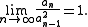
surveys progress related to this conjecture; see also .
Divisibility and factorizations
If i < j, it follows from the definition that sj ≡ 1 (mod si). Therefore, every two numbers in Sylvester's sequence are relatively prime. The sequence can be used to prove that there are infinitely many prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, as any prime can divide at most one number in the sequence. More strongly, no prime factor of a number in the sequence can be congruent to 5 (mod 6), and the sequence can be used to prove that there are infinitely many primes congruent to 7 (mod 12) .
Some effort has been expended in an attempt to factor the numbers in Sylvester's sequence, but much remains unknown about their factorization. For instance, it is not known if all numbers in the sequence are squarefree
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, although all the known terms are.
As describes, it is easy to determine which Sylvester number (if any) a given prime p divides: simply compute the recurrence defining the numbers modulo p until finding either a number that is congruent to zero (mod p) or finding a repeated modulus. Via this technique he found that 1166 out of the first three million primes are divisors of Sylvester numbers, and that none of these primes has a square that divides a Sylvester number. A general result of implies that the set of prime factors of Sylvester numbers has density zero in the set of all primes.
The following table shows known factorizations of these numbers, (except the first four, which are all prime):
| n | Factors of sn |
|---|---|
| 4 | 13 × 139 |
| 5 | 3263443, which is prime |
| 6 | 547 × 607 × 1033 × 31051 |
| 7 | 29881 × 67003 × 9119521 × 6212157481 |
| 8 | 5295435634831 × 31401519357481261 × 77366930214021991992277 |
| 9 | 181 181 (number) 181 is the natural number between 180 and 182.-In mathematics:* 181 is an odd number* 181 is a centered number** 181 is a centered pentagonal number** 181 is a centered 12-gonal number** 181 is a centered 18-gonal number... × 1987 × 112374829138729 × 114152531605972711 × P68 |
| 10 | 2287 × 2271427 × 21430986826194127130578627950810640891005487 × P156 |
| 11 | 73 73 (number) 73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :... × C416 |
| 12 | 2589377038614498251653 × 2872413602289671035947763837 × C785 |
| 13 | 52387 × 5020387 × 5783021473 × 401472621488821859737 × 287001545675964617409598279 × C1600 |
| 14 | 13999 × 74203 × 9638659 × 57218683 × 10861631274478494529 × C3293 |
| 15 | 17881 × 97822786011310111 × 54062008753544850522999875710411 × C6618 |
| 16 | 128551 × C13335 |
| 17 | 635263 × 1286773 × 21269959 × C26661 |
| 18 | 50201023123 × 139263586549 × C53339 |
| 19 | C106721 |
| 20 | 352867 × 6210298470888313 × C213419 |
| 21 | 387347773 × 1620516511 × C426863 |
| 22 | 91798039513 × C853750 |
As is customary, Pn and Cn denote prime and composite numbers n digits long.
Applications
use the properties of Sylvester's sequence to define large numbers of SasakianSasakian manifold
In differential geometry, a Sasakian manifold is a contact manifold equipped with a special kind of Riemannian metric g, called a Sasakian metric.-Definition:...
Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
s having the differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
of odd-dimensional spheres
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
or exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s. They show that the number of distinct Sasakian Einstein metrics on a topological sphere of dimension 2n − 1 is at least proportional to sn and hence has double exponential growth with n.
As describe, and used values derived from Sylvester's sequence to construct lower bound examples for online
Online algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
bin packing algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. similarly use the sequence to lower bound the performance of a two-dimensional cutting stock algorithm.
Znám's problem
Znám's problem
In number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other...
concerns sets of numbers such that each number in the set divides but is not equal to the product of all the other numbers, plus one. Without the inequality requirement, the values in Sylvester's sequence would solve the problem; with that requirement, it has other solutions derived from recurrences similar to the one defining Sylvester's sequence. Solutions to Znám's problem have applications to the classification of surface singularities (Brenton and Hill 1988) and to the theory of nondeterministic finite automata.
describes an application of the closest approximations to one by k-term sums of unit fractions, in lower-bounding the number of divisors of any perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
, and uses the same property to lower bound the size of certain groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
External links
- Irrationality of Quadratic Sums, from K. S. Brown's MathPages.

