
Sasakian manifold
Encyclopedia
In differential geometry, a Sasakian manifold (named after Shigeo Sasaki
) is a contact manifold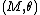 equipped with a special kind of Riemannian metric
equipped with a special kind of Riemannian metric 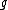 , called a Sasakian metric.
, called a Sasakian metric.
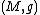 , its Riemannian cone is a product
, its Riemannian cone is a product

of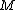 with a half-line
with a half-line 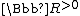 ,
,
equipped with the cone metric
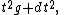
where is the parameter in
is the parameter in 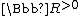 .
.
A manifold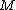 equipped with a 1-form
equipped with a 1-form 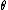
is contact if and only if the 2-form
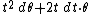
on its cone is symplectic (this is one of the possible
definitions of a contact structure). A contact Riemannian manifold is
Sasakian, if its Riemannian cone with the cone metric is a Kähler manifold
with
Kähler form
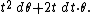

where the right hand side is a natural Kähler manifold and read as the cone over the sphere (endowed with embedded metric). The contact 1-form on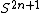 is the form associated to the tangent vector
is the form associated to the tangent vector 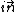 , constructued from the unit-normal vector
, constructued from the unit-normal vector 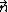 to the sphere (
to the sphere (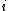 being the complex structure on
being the complex structure on  ).
).
Another non-compact example is with coordinates
with coordinates 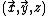 endowed with
endowed with
contact-form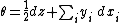 and
and
the Riemannian metric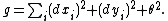
As a third example consider

where the right hand side has a natural Kähler structure (and the acts by reflection at the origin).
acts by reflection at the origin).
. There was not much activity in this field after the mid-1970s, until the advent of String theory
. Since then Sasakian manifolds have gained prominence in physics and algebraic geometry, mostly due to a string of papers by Boyer, Galicki and their co-authors.
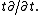
As the cone is by definition Kähler, there exists a complex structure J. The Reeb vector field on the Sasaskian manifold is defined to be
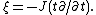
It is nowhere vanishing. It commutes with all holomorphic Killing vectors on the cone and in particular with all isometries
of the Sasakian manifold. If the orbits of the vector field close then the space of orbits is a Kähler orbifold. The Reeb vector field at the Sasakian manifold at unit radius is a unit vector field and tangential to the embedding.
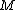 is one with the Riemannian cone Kähler.
is one with the Riemannian cone Kähler.
If the cone is, in addition, Ricci-flat, is called Sasaki–Einstein; if it is hyperkähler
is called Sasaki–Einstein; if it is hyperkähler
,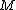 is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.
is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.
Examples include all round odd-dimensional spheres, and the product of a 2-sphere and a 3-sphere with a homogeneous metric. The cones are respectively complex vector space
s without the origin, and the conifold
.
It is also known that there exist Sasaki-Einstein metrics on some circle bundles over the 3rd through 8th del Pezzo surface
s.
In 2005 an infinite family of 5-dimensional Sasaki-Einstein metrics was constructed. These are denoted
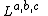
where a, b and c are three integral parameters. A 2-parameter family had been constructed the previous year, before which only a finite number of 5-dimensional examples were known.
Shigeo Sasaki
Shigeo Sasaki was a Japanese mathematician working on differential geometry who introduced Sasaki manifolds.-References:...
) is a contact manifold
 equipped with a special kind of Riemannian metric
equipped with a special kind of Riemannian metric 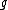 , called a Sasakian metric.
, called a Sasakian metric.Definition
A Sasakian metric is defined using the construction of the Riemannian cone. Given a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
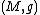 , its Riemannian cone is a product
, its Riemannian cone is a product
of
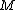 with a half-line
with a half-line 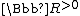 ,
,equipped with the cone metric
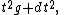
where
 is the parameter in
is the parameter in 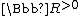 .
.A manifold
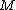 equipped with a 1-form
equipped with a 1-form 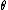
is contact if and only if the 2-form
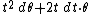
on its cone is symplectic (this is one of the possible
definitions of a contact structure). A contact Riemannian manifold is
Sasakian, if its Riemannian cone with the cone metric is a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
with
Kähler form
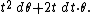
Examples
As an example consider
where the right hand side is a natural Kähler manifold and read as the cone over the sphere (endowed with embedded metric). The contact 1-form on
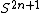 is the form associated to the tangent vector
is the form associated to the tangent vector 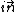 , constructued from the unit-normal vector
, constructued from the unit-normal vector 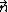 to the sphere (
to the sphere (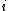 being the complex structure on
being the complex structure on  ).
).Another non-compact example is
 with coordinates
with coordinates 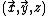 endowed with
endowed withcontact-form
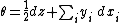 and
andthe Riemannian metric
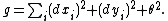
As a third example consider

where the right hand side has a natural Kähler structure (and the
 acts by reflection at the origin).
acts by reflection at the origin).History
Sasakian manifolds were introduced in 1960 by the Japanese geometer Shigeo SasakiShigeo Sasaki
Shigeo Sasaki was a Japanese mathematician working on differential geometry who introduced Sasaki manifolds.-References:...
. There was not much activity in this field after the mid-1970s, until the advent of String theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. Since then Sasakian manifolds have gained prominence in physics and algebraic geometry, mostly due to a string of papers by Boyer, Galicki and their co-authors.
The Reeb vector field
The homothetic vector field on the cone over a Sasakian manifold is defined to be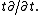
As the cone is by definition Kähler, there exists a complex structure J. The Reeb vector field on the Sasaskian manifold is defined to be
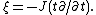
It is nowhere vanishing. It commutes with all holomorphic Killing vectors on the cone and in particular with all isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Sasakian manifold. If the orbits of the vector field close then the space of orbits is a Kähler orbifold. The Reeb vector field at the Sasakian manifold at unit radius is a unit vector field and tangential to the embedding.
Sasaki–Einstein manifolds
A Sasakian manifold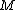 is one with the Riemannian cone Kähler.
is one with the Riemannian cone Kähler.If the cone is, in addition, Ricci-flat,
 is called Sasaki–Einstein; if it is hyperkähler
is called Sasaki–Einstein; if it is hyperkählerHyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
,
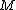 is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.
is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.Examples include all round odd-dimensional spheres, and the product of a 2-sphere and a 3-sphere with a homogeneous metric. The cones are respectively complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s without the origin, and the conifold
Conifold
In mathematics and string theory, a conifold is a generalization of a manifold. Unlike manifolds, conifolds can contain conical singularities i.e. points whose neighbourhoods look like cones over a certain base...
.
It is also known that there exist Sasaki-Einstein metrics on some circle bundles over the 3rd through 8th del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s.
In 2005 an infinite family of 5-dimensional Sasaki-Einstein metrics was constructed. These are denoted
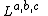
where a, b and c are three integral parameters. A 2-parameter family had been constructed the previous year, before which only a finite number of 5-dimensional examples were known.

