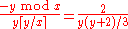Greedy algorithm for Egyptian fractions
Encyclopedia
In mathematics
, the greedy algorithm for Egyptian fractions is a greedy algorithm
, first described by Fibonacci
, for transforming rational number
s into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction
as a sum of unit fraction
s, as e.g. 5/6 = 1/2 + 1/3. As the name indicates, these representations have been used as long ago as ancient Egypt
, but the first published systematic method for constructing such expansions is described in the Liber Abaci
(1202) of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction
that can be used in any representation of the remaining fraction.
Fibonacci actually lists several different methods for constructing Egyptian fraction representations (Sigler 2002, chapter II.7). He includes the greedy method as a last resort for situations when several simpler methods fail; see Egyptian fraction for a more detailed listing of these methods. As Salzer (1948) details, the greedy method, and extensions of it for the approximation of irrational numbers, have been rediscovered several times by modern mathematicians, earliest and most notably by Sylvester
(1880); see for instance Cahen (1891) and Spiess (1907). A closely related expansion method that produces closer approximations at each step by allowing some unit fractions in the sum to be negative dates back to Lambert (1770).
The expansion produced by this method for a number x is called the greedy Egyptian expansion, Sylvester expansion, or Fibonacci–Sylvester expansion of x. However, the term Fibonacci expansion usually refers, not to this method, but to representation of integers as sums of Fibonacci number
s.
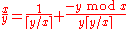
(simplifying the second term in this replacement as necessary). For instance: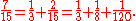
in this expansion, the denominator 3 of the first unit fraction is the result of rounding 15/7 up to the next larger integer, and the remaining fraction 2/15 is the result of simplifying (-15 mod 7)/15×3 = 6/45. The denominator of the second unit fraction, 8, is the result of rounding 15/2 up to the next larger integer, and the remaining fraction 1/120 is what is left from 7/15 after subtracting both 1/3 and 1/8.
As each expansion step reduces the numerator of the remaining fraction to be expanded, this method always terminates with a finite expansion; however, compared to ancient Egyptian expansions or to more modern methods, this method may produce expansions that are quite long, with large denominators. For instance, this method expands
while other methods lead to the much better expansion
Wagon (1991) suggests an even more badly-behaved example, 31/311. The greedy method leads to an expansion with ten terms, the last of which has over 500 digits in its denominator; however, 31/311 has a much shorter non-greedy representation, 1/12 + 1/63 + 1/2799 + 1/8708.
2, 3, 7, 43, 1807, ... can be viewed as generated by an infinite greedy expansion of this type for the number one, where at each step we choose the denominator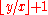 instead of
instead of 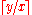 . Truncating this sequence to k terms and forming the corresponding Egyptian fraction, e.g. (for k = 4)
. Truncating this sequence to k terms and forming the corresponding Egyptian fraction, e.g. (for k = 4)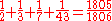
results in the closest possible underestimate of 1 by any k-term Egyptian fraction (Curtiss 1922; Soundararajan 2005). That is, for example, any Egyptian fraction for a number in the open interval (1805/1806,1) requires at least five terms. Curtiss (1922) describes an application of these closest-approximation results in lower-bounding the number of divisors of a perfect number
, while Stong (1983) describes applications in group theory
.
More generally the sequence of the smallest denominators y leading to the longest expansion for each x is
based on the greedy method. Their algorithm computes the greedy expansion of a root; at each step in this expansion it maintains an auxiliary polynomial that has as its root the remaining fraction to be expanded. Consider as an example applying this method to find the greedy expansion of the golden ratio
, one of the two solutions of the polynomial equation P0(x) = x2 - x - 1 = 0. The algorithm of Stratemeyer and Salzer performs the following sequence of steps:
Continuing this approximation process eventually produces the greedy expansion for the golden ratio,
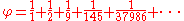 .
.
as sequences , , and , respectively. In addition, the greedy expansion of any irrational number
leads to an infinite increasing sequence of integers, and the OEIS contains expansions of several well known constants. Some additional entries in the OEIS, though not labeled as being produced by the greedy algorithm, appear to be of the same type.
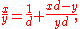
where d is chosen, among all possible values satisfying the constraints, as small as possible such that xd > y and such that d is distinct from all previously chosen denominators. For instance, the Engel expansion can be viewed as an algorithm of this type in which each successive denominator must be a multiple of the previous one. However, it may be difficult to determine whether an algorithm of this type can always succeed in finding a finite expansion. In particular, the odd greedy expansion of a fraction x/y is formed by a greedy algorithm of this type in which all denominators are constrained to be odd numbers; it is known that, whenever y is odd, there is a finite Egyptian fraction expansion in which all denominators are odd, but it is not known whether the odd greedy expansion is always finite.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the greedy algorithm for Egyptian fractions is a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
, first described by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, for transforming rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction
Irreducible fraction
An irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
as a sum of unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s, as e.g. 5/6 = 1/2 + 1/3. As the name indicates, these representations have been used as long ago as ancient Egypt
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
, but the first published systematic method for constructing such expansions is described in the Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
(1202) of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
that can be used in any representation of the remaining fraction.
Fibonacci actually lists several different methods for constructing Egyptian fraction representations (Sigler 2002, chapter II.7). He includes the greedy method as a last resort for situations when several simpler methods fail; see Egyptian fraction for a more detailed listing of these methods. As Salzer (1948) details, the greedy method, and extensions of it for the approximation of irrational numbers, have been rediscovered several times by modern mathematicians, earliest and most notably by Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
(1880); see for instance Cahen (1891) and Spiess (1907). A closely related expansion method that produces closer approximations at each step by allowing some unit fractions in the sum to be negative dates back to Lambert (1770).
The expansion produced by this method for a number x is called the greedy Egyptian expansion, Sylvester expansion, or Fibonacci–Sylvester expansion of x. However, the term Fibonacci expansion usually refers, not to this method, but to representation of integers as sums of Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
Algorithm and examples
Fibonacci's algorithm expands the fraction x/y to be represented, by repeatedly performing the replacement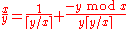
(simplifying the second term in this replacement as necessary). For instance:
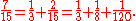
in this expansion, the denominator 3 of the first unit fraction is the result of rounding 15/7 up to the next larger integer, and the remaining fraction 2/15 is the result of simplifying (-15 mod 7)/15×3 = 6/45. The denominator of the second unit fraction, 8, is the result of rounding 15/2 up to the next larger integer, and the remaining fraction 1/120 is what is left from 7/15 after subtracting both 1/3 and 1/8.
As each expansion step reduces the numerator of the remaining fraction to be expanded, this method always terminates with a finite expansion; however, compared to ancient Egyptian expansions or to more modern methods, this method may produce expansions that are quite long, with large denominators. For instance, this method expands

while other methods lead to the much better expansion

Wagon (1991) suggests an even more badly-behaved example, 31/311. The greedy method leads to an expansion with ten terms, the last of which has over 500 digits in its denominator; however, 31/311 has a much shorter non-greedy representation, 1/12 + 1/63 + 1/2799 + 1/8708.
Sylvester's sequence and closest approximation
Sylvester's sequenceSylvester's sequence
In number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
2, 3, 7, 43, 1807, ... can be viewed as generated by an infinite greedy expansion of this type for the number one, where at each step we choose the denominator
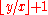 instead of
instead of 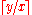 . Truncating this sequence to k terms and forming the corresponding Egyptian fraction, e.g. (for k = 4)
. Truncating this sequence to k terms and forming the corresponding Egyptian fraction, e.g. (for k = 4)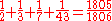
results in the closest possible underestimate of 1 by any k-term Egyptian fraction (Curtiss 1922; Soundararajan 2005). That is, for example, any Egyptian fraction for a number in the open interval (1805/1806,1) requires at least five terms. Curtiss (1922) describes an application of these closest-approximation results in lower-bounding the number of divisors of a perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
, while Stong (1983) describes applications in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
Maximum-length expansions and congruence conditions
Any fraction x/y requires at most x terms in its greedy expansion. Mays (1987) and Freitag and Phillips (1999) examine the conditions under which x/y leads to an expansion with exactly x terms; these can be described in terms of congruence conditions on y.- Every fraction 1/y requires one term in its expansion; the simplest such fraction is 1/1.
- Every fraction 2/y for odd y > 1 requires two terms in its expansion; the simplest such fraction is 2/3.
- A fraction 3/y requires three terms in its expansion if and only if y ≡ 1 (mod 6), for then -y mod x = 2 and y(y+2)/3 is odd, so the fraction remaining after a single step of the greedy expansion,
-
- is in simplest terms. The simplest fraction 3/y with a three-term expansion is 3/7.
- A fraction 4/y requires four terms in its expansion if and only if y ≡ 1 or 17 (mod 24), for then the numerator -y mod x of the remaining fraction is 3 and the denominator is 1 (mod 6). The simplest fraction 4/y with a four-term expansion is 4/17. The Erdős–Straus conjectureErdos–Straus conjectureIn number theory, the Erdős–Straus conjecture states that for all integers n ≥ 2, the rational number 4/n can be expressed as the sum of three unit fractions. Paul Erdős and Ernst G...
states that all fractions 4/y have an expansion with three or fewer terms, but when y ≡ 1 or 17 (mod 24) such expansions must be found by methods other than the greedy algorithm.
More generally the sequence of the smallest denominators y leading to the longest expansion for each x is
- 1, 3, 7, 17, 31, 109, 253, 97, 271, ... .
Approximation of polynomial roots
Stratemeyer (1930) and Salzer (1947) describe a method of finding an accurate approximation for the roots of a polynomialRoot-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
based on the greedy method. Their algorithm computes the greedy expansion of a root; at each step in this expansion it maintains an auxiliary polynomial that has as its root the remaining fraction to be expanded. Consider as an example applying this method to find the greedy expansion of the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, one of the two solutions of the polynomial equation P0(x) = x2 - x - 1 = 0. The algorithm of Stratemeyer and Salzer performs the following sequence of steps:
- Since P0(x) < 0 for x = 1, and P0(x) > 0 for all x ≥ 2, there must be a root of P0(x) between 1 and 2. That is, the first term of the greedy expansion of the golden ratio is 1/1. If x1 is the remaining fraction after the first step of the greedy expansion, it satisfies the equation P0(x1 + 1) = 0, which can be expanded as P1(x1) = x12 + x1 - 1 = 0.
- Since P1(x) < 0 for x = 1/2, and P1(x) > 0 for all x > 1, the root of P1 lies between 1/2 and 1, and the first term in its greedy expansion (the second term in the greedy expansion for the golden ratio) is 1/2. If x2 is the remaining fraction after this step of the greedy expansion, it satisfies the equation P1(x2 + 1/2) = 0, which can be expanded as P2(x2) = 4x22 + 8x2 - 1 = 0.
- Since P2(x) < 0 for x = 1/9, and P2(x) > 0 for all x > 1/8, the next term in the greedy expansion is 1/9. If x3 is the remaining fraction after this step of the greedy expansion, it satisfies the equation P2(x3 + 1/9) = 0, which can again be expanded as a polynomial equation with integer coefficients, P3(x3) = 324x32 + 720x3 - 5 = 0.
Continuing this approximation process eventually produces the greedy expansion for the golden ratio,
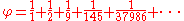 .
.Other integer sequences
The length, minimum denominator, and maximum denominator of the greedy expansion for all fractions with small numerators and denominators can be found in the On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
as sequences , , and , respectively. In addition, the greedy expansion of any irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
leads to an infinite increasing sequence of integers, and the OEIS contains expansions of several well known constants. Some additional entries in the OEIS, though not labeled as being produced by the greedy algorithm, appear to be of the same type.
Related expansions
In general, if one wants an Egyptian fraction expansion in which the denominators are constrained in some way, it is possible to define a greedy algorithm in which at each step one chooses the expansion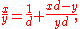
where d is chosen, among all possible values satisfying the constraints, as small as possible such that xd > y and such that d is distinct from all previously chosen denominators. For instance, the Engel expansion can be viewed as an algorithm of this type in which each successive denominator must be a multiple of the previous one. However, it may be difficult to determine whether an algorithm of this type can always succeed in finding a finite expansion. In particular, the odd greedy expansion of a fraction x/y is formed by a greedy algorithm of this type in which all denominators are constrained to be odd numbers; it is known that, whenever y is odd, there is a finite Egyptian fraction expansion in which all denominators are odd, but it is not known whether the odd greedy expansion is always finite.