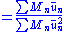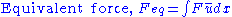
Structural Dynamics
Encyclopedia
Structural dynamics is a subset of structural analysis
which covers the behaviour of structure
s subjected to dynamic loading. Dynamic loads include people, wind, waves, traffic, earthquake
s, and blasts. Any structure can be subject to dynamic loading. Dynamic analysis can be used to find dynamic displacements
, time history, and modal analysis
.
A static
load is one which does not vary. A dynamic load is one which changes with time. If it changes slowly, the structure's response may be determined with static analysis, but if it varies quickly (relative to the structure's ability to respond), the response must be determined with a dynamic analysis.
Dynamic analysis for simple structures can be carried out manually, but for complex structures finite element analysis can be used to calculate the mode shapes and frequencies. An open-source, lightweight, free software DYSSOLVE can be used to solve basic structural dynamics problems.
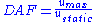
where u is the deflection of the structure due to the applied load.
Graphs of dynamic amplification factors vs non-dimensional rise time
(tr/T) exist for standard loading functions (for an explanation of rise time, see time history analysis below). Hence the DAF for a given loading can be read from the graph, the static deflection can be easily calculated for simple structures and the dynamic deflection found.
.
A simple single degree of freedom
system
(a mass
, M, on a spring
of stiffness
, k for example) has the following equation of motion:
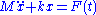
where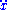
is the acceleration (the double derivative
of the displacement) and x is the displacement.
If the loading F(t) is a Heaviside step function
(the sudden application of a constant load), the solution to the equation of motion is:
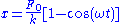
where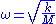
and the fundamental natural frequency, 
.
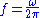The static deflection of a single degree of freedom system is:
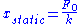
so you can write, by combining the above formulae:
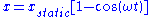
This gives the (theoretical) time history of the structure due to a load F(t), where the false assumption is made that there is no damping
.
Although this is too simplistic to apply to a real structure, the Heaviside Step Function is a reasonable model for the application of many real loads, such as the sudden addition of a piece of furniture, or the removal of a prop to a newly cast concrete floor. However, in reality loads are never applied instantaneously - they build up over a period of time (this may be very short indeed). This time is called the rise time
.
As the number of degrees of freedom of a structure increases it very quickly becomes too difficult to calculate the time history manually - real structures are analysed using non-linear finite element analysis software.
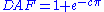
where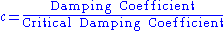
and is typically 2%-10% depending on the type of construction:
Generally damping would be ignored for non-transient events (such as wind loading or crowd loading), but would be important for transient events (for example, an impulse load such as a bomb blast).
calculates the frequency modes
or natural frequencies of a given system, but not necessarily its full time history response to a given input. The natural frequency of a system is dependent only on the stiffness
of the structure and the mass
which participates with the structure (including self-weight). It is not dependent on the load function.
It is useful to know the modal frequencies of a structure as it allows you to ensure that the frequency of any applied periodic loading will not coincide with a modal frequency and hence cause resonance
, which leads to large oscillations.
The method is:
. For a given mode shape of a multiple degree of freedom system you can find an "equivalent" mass, stiffness and applied force for a single degree of freedom system. For simple structures the basic mode shapes can be found by inspection, but it is not a conservative method. Rayleigh's principle states:
"The frequency ω of an arbitrary mode of vibration, calculated by the energy method, is always greater than - or equal to - the fundamental frequency ωn."
For an assumed mode shape
, of a structural system with mass, M; stiffness, EI (Young's modulus
, E, multiplied by the second moment of area
, I); and applied force, F(x):
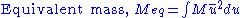
then, as above:
. The summation can be carried out by one of three common methods:
To superpose the individual modal responses manually, having calculated them by the energy method:
Assuming that the rise time tr is known (T = 2π/ω), it is possible to read the DAF from a standard graph. The static displacement can be calculated with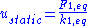
. The dynamic displacement for the chosen mode and applied force can then be found from:
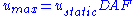
(such as the mass of ground in an earthquake
) and mass participating in inertia
effects (the mass of the structure itself, Meq). The modal participation factor Γ is a comparison of these two masses. For a single degree of freedom system Γ = 1.
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
which covers the behaviour of structure
Structure
Structure is a fundamental, tangible or intangible notion referring to the recognition, observation, nature, and permanence of patterns and relationships of entities. This notion may itself be an object, such as a built structure, or an attribute, such as the structure of society...
s subjected to dynamic loading. Dynamic loads include people, wind, waves, traffic, earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
s, and blasts. Any structure can be subject to dynamic loading. Dynamic analysis can be used to find dynamic displacements
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, time history, and modal analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
.
A static
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
load is one which does not vary. A dynamic load is one which changes with time. If it changes slowly, the structure's response may be determined with static analysis, but if it varies quickly (relative to the structure's ability to respond), the response must be determined with a dynamic analysis.
Dynamic analysis for simple structures can be carried out manually, but for complex structures finite element analysis can be used to calculate the mode shapes and frequencies. An open-source, lightweight, free software DYSSOLVE can be used to solve basic structural dynamics problems.
Displacements
A dynamic load can have a significantly larger effect than a static load of the same magnitude due to the structure's inability to respond quickly to the loading (by deflecting). The increase in the effect of a dynamic load is given by the dynamic amplification factor (DAF):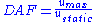where u is the deflection of the structure due to the applied load.
Graphs of dynamic amplification factors vs non-dimensional rise time
Rise time
In electronics, when describing a voltage or current step function, rise time refers to the time required for a signal to change from a specified low value to a specified high value...
(tr/T) exist for standard loading functions (for an explanation of rise time, see time history analysis below). Hence the DAF for a given loading can be read from the graph, the static deflection can be easily calculated for simple structures and the dynamic deflection found.
Time history analysis
A full time history will give the response of a structure over time during and after the application of a load. To find the full time history of a structure's response you must solve the structure's equation of motionEquation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
.
Example
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
system
System
System is a set of interacting or interdependent components forming an integrated whole....
(a mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, M, on a spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
of stiffness
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
, k for example) has the following equation of motion:
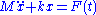
where
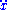is the acceleration (the double derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the displacement) and x is the displacement.
If the loading F(t) is a Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
(the sudden application of a constant load), the solution to the equation of motion is:
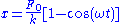
where
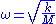and the fundamental natural frequency, 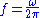.The static deflection of a single degree of freedom system is:
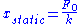
so you can write, by combining the above formulae:
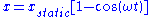
This gives the (theoretical) time history of the structure due to a load F(t), where the false assumption is made that there is no damping
Damping
In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
.
Although this is too simplistic to apply to a real structure, the Heaviside Step Function is a reasonable model for the application of many real loads, such as the sudden addition of a piece of furniture, or the removal of a prop to a newly cast concrete floor. However, in reality loads are never applied instantaneously - they build up over a period of time (this may be very short indeed). This time is called the rise time
Rise time
In electronics, when describing a voltage or current step function, rise time refers to the time required for a signal to change from a specified low value to a specified high value...
.
As the number of degrees of freedom of a structure increases it very quickly becomes too difficult to calculate the time history manually - real structures are analysed using non-linear finite element analysis software.
Damping
Any real structure will dissipate energy (mainly through friction). This can be modelled by modifying the DAF: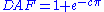where
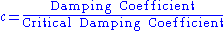and is typically 2%-10% depending on the type of construction:- Bolted steel ~6%
- Reinforced concrete ~ 5%
- Welded steel ~ 2%
Generally damping would be ignored for non-transient events (such as wind loading or crowd loading), but would be important for transient events (for example, an impulse load such as a bomb blast).
Modal analysis
A modal analysisModal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
calculates the frequency modes
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
or natural frequencies of a given system, but not necessarily its full time history response to a given input. The natural frequency of a system is dependent only on the stiffness
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
of the structure and the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
which participates with the structure (including self-weight). It is not dependent on the load function.
It is useful to know the modal frequencies of a structure as it allows you to ensure that the frequency of any applied periodic loading will not coincide with a modal frequency and hence cause resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
, which leads to large oscillations.
The method is:
- Find the natural modes (the shape adopted by a structure) and natural frequencies
- Calculate the response of each mode
- Optionally superpose the response of each mode to find the full modal response to a given loading
Energy method
It is possible to calculate the frequency of different mode shapes of system manually by the energy methodEnergy principles in structural mechanics
Energy principles in structural mechanics express the relationships between stresses, strains or deformations, displacements, material properties, and external effects in the form of energy or work done by internal and external forces...
. For a given mode shape of a multiple degree of freedom system you can find an "equivalent" mass, stiffness and applied force for a single degree of freedom system. For simple structures the basic mode shapes can be found by inspection, but it is not a conservative method. Rayleigh's principle states:
"The frequency ω of an arbitrary mode of vibration, calculated by the energy method, is always greater than - or equal to - the fundamental frequency ωn."
For an assumed mode shape
, of a structural system with mass, M; stiffness, EI (Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
, E, multiplied by the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
, I); and applied force, F(x):
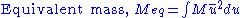
then, as above:
Modal response
The complete modal response to a given load F(x,t) is. The summation can be carried out by one of three common methods:- Superpose complete time histories of each mode (time consuming, but exact)
- Superpose the maximum amplitudes of each mode (quick but conservative)
- Superpose the square root of the sum of squares (good estimate for well-separated frequencies, but unsafe for closely spaced frequencies)
To superpose the individual modal responses manually, having calculated them by the energy method:
Assuming that the rise time tr is known (T = 2π/ω), it is possible to read the DAF from a standard graph. The static displacement can be calculated with
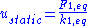. The dynamic displacement for the chosen mode and applied force can then be found from: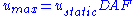Modal participation factor
For real systems there is often mass participating in the forcing functionForcing function
Forcing function can mean:* In differential calculus, a Forcing function * In interaction design, a behavior-shaping constraint, a means of preventing undesirable user input usually made by mistake....
(such as the mass of ground in an earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
) and mass participating in inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
effects (the mass of the structure itself, Meq). The modal participation factor Γ is a comparison of these two masses. For a single degree of freedom system Γ = 1.
- Γ
