
Fock space
Encyclopedia
The Fock space is an algebra
ic system used in quantum mechanics
to describe quantum states with a variable or unknown number of particles
. It is named after V. A. Fock
who first introduced it in his paper Konfigurationsraum und zweite Quantelung.
Technically, the Fock space is the Hilbert space
made from the direct sum
of
tensor product
s of single-particle Hilbert spaces:
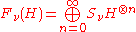
where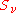 is the operator which symmetrizes or antisymmetrizes the space, depending on whether the Hilbert space describes particles obeying boson
is the operator which symmetrizes or antisymmetrizes the space, depending on whether the Hilbert space describes particles obeying boson
ic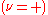 or fermion
or fermion
ic statistics respectively.
statistics respectively.  is the single particle Hilbert space. It describes the quantum states for a single particle, and to describe the quantum states of systems with
is the single particle Hilbert space. It describes the quantum states for a single particle, and to describe the quantum states of systems with  particles, or superpositions of such states, one must use a larger Hilbert space, the Fock space, which contains states for unlimited and variable number of particles. Fock state
particles, or superpositions of such states, one must use a larger Hilbert space, the Fock space, which contains states for unlimited and variable number of particles. Fock state
s are the natural basis of this space. (See also the Slater determinant
.)
of tensor product
s of copies of a single-particle Hilbert space

Here represents the states of no particles,
represents the states of no particles,  the state of one particle,
the state of one particle, 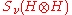 the states of two identical particles etc.
the states of two identical particles etc.
A typical state in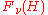 is given by
is given by

where is a complex number,
is a complex number,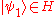 ,
,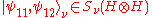 ,
,
etc.
For

the inner product on is defined as
is defined as
where we use the inner products on each of the -particle Hilbert spaces.
-particle Hilbert spaces.
The convergence of this infinite sum is important if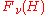 is to be a Hilbert space. Technically we require
is to be a Hilbert space. Technically we require 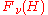 to be the subspace of
to be the subspace of 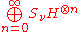 which consists of all vectors with finite norm
which consists of all vectors with finite norm
(where the norm is defined by the inner product as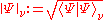 ).
).

describing particles, one of which has wavefunction
particles, one of which has wavefunction
 , another
, another 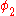 and so on up to the
and so on up to the  th particle, where each
th particle, where each 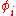 is any wavefunction from the single particle Hilbert space
is any wavefunction from the single particle Hilbert space  . When we speak of one particle in state
. When we speak of one particle in state 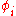 , it must be borne in mind that in quantum mechanics identical particles are indistinguishable
, it must be borne in mind that in quantum mechanics identical particles are indistinguishable
, and in the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are intrinsically properly symmetrized. So that for instance, if the above state is fermionic, it will be 0 if two (or more) of the
is fermionic, it will be 0 if two (or more) of the 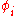 are equal, because by the Pauli exclusion principle
are equal, because by the Pauli exclusion principle
no two (or more) fermions can be in the same quantum state. Also, the states are properly normalized, by construction.
A useful and convenient basis for this space is the occupancy number basis. If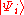 is a basis of
is a basis of  , then we can agree to denote the state with
, then we can agree to denote the state with  particles in state
particles in state 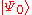 ,
,
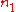 particles in state
particles in state 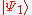 , ...,
, ...,
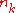 particles in state
particles in state 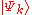 by
by

with each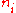 taking the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles.
taking the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles.
Such a state is called a Fock state
. Since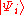 are understood as the steady states of the free field, i.e., a definite number of particles, a Fock state describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
are understood as the steady states of the free field, i.e., a definite number of particles, a Fock state describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
Two operators of paramount importance are the creation and annihilation operators
, which upon acting on a Fock state respectively add and remove a particle in the ascribed quantum state. They are denoted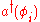 and
and 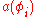 respectively, with
respectively, with 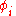 referring to the quantum state
referring to the quantum state 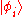 in which the particle is removed or added. It is often convenient to work with states of the basis of
in which the particle is removed or added. It is often convenient to work with states of the basis of  so that these operators remove and add exactly one particle in the given state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state
so that these operators remove and add exactly one particle in the given state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state 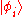 is
is 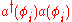 .
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic system used in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to describe quantum states with a variable or unknown number of particles
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
. It is named after V. A. Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
who first introduced it in his paper Konfigurationsraum und zweite Quantelung.
Technically, the Fock space is the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
made from the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of
tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of single-particle Hilbert spaces:
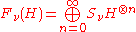
where
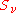 is the operator which symmetrizes or antisymmetrizes the space, depending on whether the Hilbert space describes particles obeying boson
is the operator which symmetrizes or antisymmetrizes the space, depending on whether the Hilbert space describes particles obeying bosonBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic
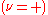 or fermion
or fermionFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic
 statistics respectively.
statistics respectively.  is the single particle Hilbert space. It describes the quantum states for a single particle, and to describe the quantum states of systems with
is the single particle Hilbert space. It describes the quantum states for a single particle, and to describe the quantum states of systems with  particles, or superpositions of such states, one must use a larger Hilbert space, the Fock space, which contains states for unlimited and variable number of particles. Fock state
particles, or superpositions of such states, one must use a larger Hilbert space, the Fock space, which contains states for unlimited and variable number of particles. Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
s are the natural basis of this space. (See also the Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
.)
Definition
Fock space is the direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of copies of a single-particle Hilbert space


Here
 represents the states of no particles,
represents the states of no particles,  the state of one particle,
the state of one particle, 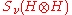 the states of two identical particles etc.
the states of two identical particles etc.A typical state in
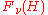 is given by
is given by
where
 is a complex number,
is a complex number,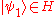 ,
,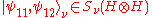 ,
,etc.
For


the inner product on
 is defined as
is defined as
where we use the inner products on each of the
 -particle Hilbert spaces.
-particle Hilbert spaces.The convergence of this infinite sum is important if
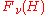 is to be a Hilbert space. Technically we require
is to be a Hilbert space. Technically we require 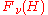 to be the subspace of
to be the subspace of 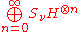 which consists of all vectors with finite norm
which consists of all vectors with finite normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
(where the norm is defined by the inner product as
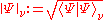 ).
).Example
An example of a state of the Fock space is
describing
 particles, one of which has wavefunction
particles, one of which has wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
 , another
, another 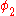 and so on up to the
and so on up to the  th particle, where each
th particle, where each 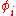 is any wavefunction from the single particle Hilbert space
is any wavefunction from the single particle Hilbert space  . When we speak of one particle in state
. When we speak of one particle in state 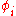 , it must be borne in mind that in quantum mechanics identical particles are indistinguishable
, it must be borne in mind that in quantum mechanics identical particles are indistinguishableIdentical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
, and in the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are intrinsically properly symmetrized. So that for instance, if the above state
 is fermionic, it will be 0 if two (or more) of the
is fermionic, it will be 0 if two (or more) of the 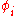 are equal, because by the Pauli exclusion principle
are equal, because by the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
no two (or more) fermions can be in the same quantum state. Also, the states are properly normalized, by construction.
A useful and convenient basis for this space is the occupancy number basis. If
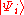 is a basis of
is a basis of  , then we can agree to denote the state with
, then we can agree to denote the state with  particles in state
particles in state 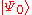 ,
,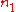 particles in state
particles in state 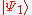 , ...,
, ...,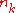 particles in state
particles in state 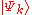 by
by
with each
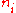 taking the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles.
taking the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles.Such a state is called a Fock state
Fock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
. Since
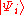 are understood as the steady states of the free field, i.e., a definite number of particles, a Fock state describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
are understood as the steady states of the free field, i.e., a definite number of particles, a Fock state describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.Two operators of paramount importance are the creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
, which upon acting on a Fock state respectively add and remove a particle in the ascribed quantum state. They are denoted
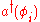 and
and 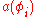 respectively, with
respectively, with 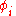 referring to the quantum state
referring to the quantum state 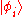 in which the particle is removed or added. It is often convenient to work with states of the basis of
in which the particle is removed or added. It is often convenient to work with states of the basis of  so that these operators remove and add exactly one particle in the given state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state
so that these operators remove and add exactly one particle in the given state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state 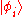 is
is 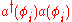 .
.See also
- BosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
- FermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
- Creation and annihilation operatorsCreation and annihilation operatorsCreation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
- Wick's theoremWick's theoremWick's theorem is a method of reducing high-order derivatives to a combinatorics problem . It is named after Gian-Carlo Wick. It is used extensively in quantum field theory to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators...
- Noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...

