String cosmology
Encyclopedia
String cosmology is a relatively new field that tries to apply equations of string theory
to solve the questions of early cosmology
. A related area of study is brane cosmology
.
This approach can be dated back to a paper by Gabriele Veneziano
that shows how an inflationary cosmological model can be obtained from string theory, thus opening the door to a description of pre-big bang
scenarios.
The idea is related to a property of the bosonic string
in a curve background, better known as nonlinear sigma model. First calculations from this model showed as the beta function
, representing the running of the metric of the model as a function of an energy scale, is proportional to the Ricci tensor giving rise to a Ricci flow
. As this model has conformal invariance
and this must be kept to have a sensible quantum field theory
, the beta function
must be zero producing immediately Einstein equations. While Einstein equations seem to appear somewhat out of place, nevertheless this result is surely striking showing as a background two-dimensional model could produce higher-dimensional physics. An interesting point here is that such a string theory can be formulated without a requirement of criticality at 26 dimensions for consistency as happens on a flat background. This is a serious hint that the underlying physics of Einstein equations could be described by an effective two-dimensional conformal field theory
. Indeed, the fact that we have evidence for an inflationary universe is an important support to string cosmology.
In the evolution of the universe, after the inflationary phase, the expansion observed today sets in that is well described by Friedmann equations
. A smooth transition is expected between these two different phases. String cosmology appears to have difficulties in explaining this transition. This is known in literature as the graceful exit problem.
An inflationary cosmology implies the presence of a scalar field that drives inflation. In string cosmology, this arises from the so-called dilaton
field. This is a scalar term entering into the description of the bosonic string
that produces a scalar field term into the effective theory at low energies. The corresponding equations resemble those of a Brans-Dicke theory
.
Analysis has been worked out from a critical number of dimension (26) down to four. In general one gets Friedmann equations
in an arbitrary number of dimensions. The other way round is to assume that a certain number of dimensions is compactified
producing an effective four-dimensional theory to work with. Such a theory is a typical Kaluza-Klein theory with a set of scalar fields arising from compactified
dimensions. Such fields are called moduli.
, which can be written as:
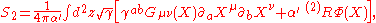
where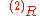
is the Ricci scalar in two dimensions, 
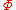the dilaton
field, and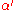
the string constant. The indices 
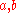range over 1,2, and 
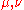over 
, where D the dimension of the target space. A further antisymmetric field could be added. This is generally considered when one wants this action generating a potential for inflation. Otherwise, a generic potential is inserted by hand, as well as a cosmological constant.
The above string action has a conformal invariance. This is a property of a two dimensional Riemannian manifold
. At the quantum level, this property is lost due to anomalies and the theory itself is not consistent, having no unitarity. So it is necessary to require that conformal invariance
is kept at any order of perturbation theory
. Perturbation theory
is the only known approach to manage the quantum field theory
. Indeed, the beta functions at two loops are
and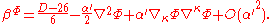
The assumption that conformal invariance
holds implies that
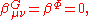
producing the corresponding equations of motion of low-energy physics. These conditions can only be satisfied perturbatively, but this has to hold at any order of perturbation theory
. The first term in
is just the anomaly of the bosonic string theory
in a flat spacetime. But here there are further terms that can grant a compensation of the anomaly also when
, and from this cosmological models of a pre-big bang scenario can be constructed. Indeed, this low energy equations can be obtained from the following action:
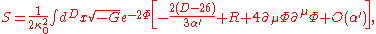
where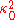
is a constant that can always be changed by redefining the dilaton field. One can also rewrite this action in a more familiar form by redefining the fields (Einstein frame) as
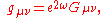
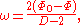
and using
one can write
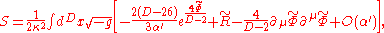
where
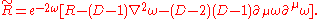
This is the formula for the Einstein action describing a scalar field interacting with a gravitational field in D dimensions. Indeed, the following identity holds:
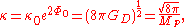
where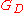
is the Newton constant in D dimensions and 
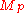the corresponding Planck mass. When setting 
in this action, the conditions for inflation are not fulfilled unless a potential or antisymmetric term is added to the string action, in which case power-law inflation is possible.
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
to solve the questions of early cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
. A related area of study is brane cosmology
Brane cosmology
Brane cosmology refers to several theories in particle physics and cosmology motivated by, but not exclusively derived from, superstring theory and M-theory.-Brane and bulk:...
.
This approach can be dated back to a paper by Gabriele Veneziano
Gabriele Veneziano
Gabriele Veneziano, born in Florence, Italy), is an Italian theoretical physicist and the founder of string theory. . Has spent most of his scientific activities at CERN in Geneva, Switzerland...
that shows how an inflationary cosmological model can be obtained from string theory, thus opening the door to a description of pre-big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
scenarios.
The idea is related to a property of the bosonic string
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
in a curve background, better known as nonlinear sigma model. First calculations from this model showed as the beta function
Beta-function
In theoretical physics, specifically quantum field theory, a beta function β encodes the dependence of a coupling parameter, g, on the energy scale, \mu of a given physical process....
, representing the running of the metric of the model as a function of an energy scale, is proportional to the Ricci tensor giving rise to a Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
. As this model has conformal invariance
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and this must be kept to have a sensible quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the beta function
Beta-function
In theoretical physics, specifically quantum field theory, a beta function β encodes the dependence of a coupling parameter, g, on the energy scale, \mu of a given physical process....
must be zero producing immediately Einstein equations. While Einstein equations seem to appear somewhat out of place, nevertheless this result is surely striking showing as a background two-dimensional model could produce higher-dimensional physics. An interesting point here is that such a string theory can be formulated without a requirement of criticality at 26 dimensions for consistency as happens on a flat background. This is a serious hint that the underlying physics of Einstein equations could be described by an effective two-dimensional conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. Indeed, the fact that we have evidence for an inflationary universe is an important support to string cosmology.
In the evolution of the universe, after the inflationary phase, the expansion observed today sets in that is well described by Friedmann equations
Friedmann equations
The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...
. A smooth transition is expected between these two different phases. String cosmology appears to have difficulties in explaining this transition. This is known in literature as the graceful exit problem.
An inflationary cosmology implies the presence of a scalar field that drives inflation. In string cosmology, this arises from the so-called dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
field. This is a scalar term entering into the description of the bosonic string
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
that produces a scalar field term into the effective theory at low energies. The corresponding equations resemble those of a Brans-Dicke theory
Brans-Dicke theory
In theoretical physics, the Brans–Dicke theory of gravitation is a theoretical framework to explain gravitation. It is a well-known competitor of Einstein's more popular theory of general relativity...
.
Analysis has been worked out from a critical number of dimension (26) down to four. In general one gets Friedmann equations
Friedmann equations
The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...
in an arbitrary number of dimensions. The other way round is to assume that a certain number of dimensions is compactified
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
producing an effective four-dimensional theory to work with. Such a theory is a typical Kaluza-Klein theory with a set of scalar fields arising from compactified
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
dimensions. Such fields are called moduli.
Technical details
This section presents some of the relevant equations entering into string cosmology. The starting point is the Polyakov actionPolyakov action
In physics, the Polyakov action is the two-dimensional action of a conformal field theory describing the worldsheet of a string in string theory...
, which can be written as:
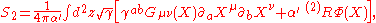
where
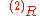is the Ricci scalar in two dimensions, 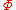the dilatonDilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
field, and
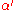the string constant. The indices 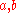range over 1,2, and 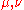over , where D the dimension of the target space. A further antisymmetric field could be added. This is generally considered when one wants this action generating a potential for inflation. Otherwise, a generic potential is inserted by hand, as well as a cosmological constant.The above string action has a conformal invariance. This is a property of a two dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. At the quantum level, this property is lost due to anomalies and the theory itself is not consistent, having no unitarity. So it is necessary to require that conformal invariance
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
is kept at any order of perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. Perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
is the only known approach to manage the quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. Indeed, the beta functions at two loops are
and
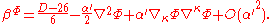
The assumption that conformal invariance
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
holds implies that
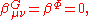
producing the corresponding equations of motion of low-energy physics. These conditions can only be satisfied perturbatively, but this has to hold at any order of perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. The first term in
is just the anomaly of the bosonic string theoryBosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
in a flat spacetime. But here there are further terms that can grant a compensation of the anomaly also when
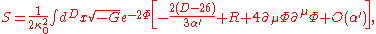
, and from this cosmological models of a pre-big bang scenario can be constructed. Indeed, this low energy equations can be obtained from the following action:where
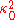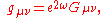
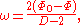
is a constant that can always be changed by redefining the dilaton field. One can also rewrite this action in a more familiar form by redefining the fields (Einstein frame) asand using
one can write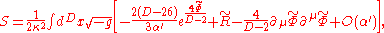where
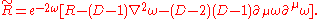
This is the formula for the Einstein action describing a scalar field interacting with a gravitational field in D dimensions. Indeed, the following identity holds:
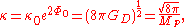
where
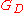is the Newton constant in D dimensions and 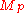the corresponding Planck mass. When setting in this action, the conditions for inflation are not fulfilled unless a potential or antisymmetric term is added to the string action, in which case power-law inflation is possible.