
Stolarsky mean
Encyclopedia
In mathematics
, the Stolarsky mean of two positive real number
s x, y is defined as:
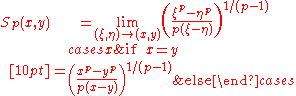
It is derived from the mean value theorem
, which states that a secant line
, cutting the graph of a differentiable function at
at 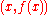 and
and 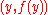 , has the same slope
, has the same slope
as a line tangent
to the graph at some point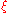 in the interval
in the interval
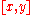 .
.
The Stolarsky mean is obtained by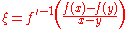
when choosing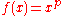 .
.
.
You obtain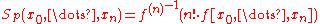 for
for 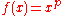 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Stolarsky mean of two positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s x, y is defined as:
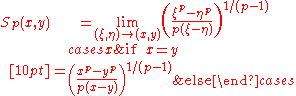
It is derived from the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, which states that a secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
, cutting the graph of a differentiable function
 at
at 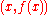 and
and 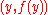 , has the same slope
, has the same slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
as a line tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the graph at some point
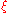 in the interval
in the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
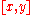 .
.
The Stolarsky mean is obtained by
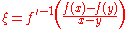
when choosing
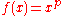 .
.Special cases
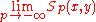 is the minimum.
is the minimum. is the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
is the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
.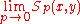 is the logarithmic meanLogarithmic meanIn mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient...
is the logarithmic meanLogarithmic meanIn mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient...
. It can be obtained from the mean value theorem by choosing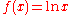 .
. is the power mean with exponent
is the power mean with exponent  .
.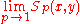 is the identric mean. It can be obtained from the mean value theorem by choosing
is the identric mean. It can be obtained from the mean value theorem by choosing  .
. is the arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
is the arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
. is a connection to the quadratic mean and the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
is a connection to the quadratic mean and the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
.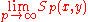 is the maximum.
is the maximum.
Generalizations
You can generalize the mean to n + 1 variables by considering the mean value theorem for divided differences for the nth derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
.
You obtain
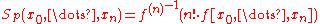 for
for 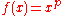 .
.

