
Logarithmic mean
Encyclopedia
In mathematics
, the logarithmic mean is a function
of two non-negative number
s which is equal to their difference
divided by the logarithm
of their quotient
. In symbols:
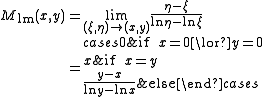
for the positive numbers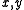 .
.
This calculation is applicable in engineering
problems involving heat
and mass transfer
.
but larger than the geometric mean
(unless the numbers are the same, in which case all three means are equal to the numbers):
the logarithmic mean is obtained as the value of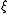
by substituting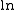 for
for 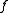
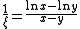
and solving for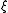 .
.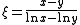
under an exponential curve
.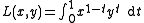
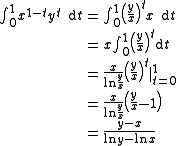
The area interpretation allows to easily derive basic properties of the logarithmic mean.
Since the exponential function is monotonic
the integral over an interval of length 1 is bounded by and
and 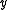 .
.
The Homogeneity
of the integral operator is transferred to the mean operator,
that is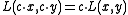 .
.
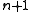 variables by considering the mean value theorem for divided differences
variables by considering the mean value theorem for divided differences
for the th derivative
th derivative
of the logarithm.
You obtain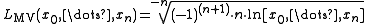
where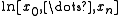 denotes a divided difference of the logarithm.
denotes a divided difference of the logarithm.
For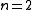 this leads to
this leads to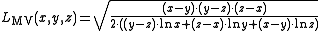 .
.
but it leads to a different result.
Given the simplex
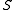
with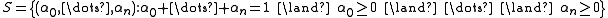 and an appropriate measure
and an appropriate measure  which assigns the simplex a volume of 1, we obtain
which assigns the simplex a volume of 1, we obtain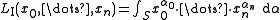
This can be simplified using divided differences of the exponential function to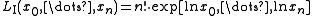 .
.
Example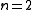
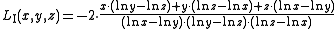 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the logarithmic mean is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of two non-negative number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s which is equal to their difference
Difference
Difference may refer to:* Difference , a 2005 power metal album* Difference , a concept in computer science* Difference , any systematic way of distinguishing similar coats of arms belonging to members of the same family* Difference , a statement about the relative size or order of two objects**...
divided by the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of their quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
. In symbols:
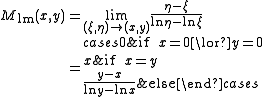
for the positive numbers
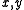 .
.This calculation is applicable in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
problems involving heat
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
and mass transfer
Mass transfer
Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...
.
Inequalities
The logarithmic mean of two numbers is smaller than the arithmetic meanArithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
but larger than the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
(unless the numbers are the same, in which case all three means are equal to the numbers):
Mean value theorem of differential calculus
From the mean value theoremMean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
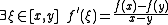
the logarithmic mean is obtained as the value of
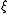
by substituting
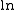 for
for 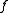
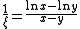
and solving for
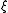 .
.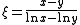
Integration
The logarithmic mean can also be interpreted as the areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
under an exponential curve
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
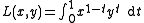
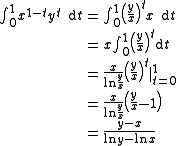
The area interpretation allows to easily derive basic properties of the logarithmic mean.
Since the exponential function is monotonic
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
the integral over an interval of length 1 is bounded by
 and
and 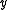 .
.The Homogeneity
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of the integral operator is transferred to the mean operator,
that is
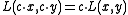 .
.Mean value theorem of differential calculus
You can generalize the mean to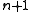 variables by considering the mean value theorem for divided differences
variables by considering the mean value theorem for divided differencesMean value theorem (divided differences)
In mathematical analysis, the mean value theorem for divided differences generalizes the mean value theorem to higher derivatives.-Statement of the theorem:...
for the
 th derivative
th derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the logarithm.
You obtain
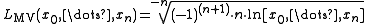
where
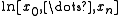 denotes a divided difference of the logarithm.
denotes a divided difference of the logarithm.For
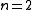 this leads to
this leads to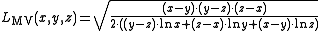 .
.Integral
The integral interpretation can also be generalized to more variables,but it leads to a different result.
Given the simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
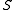
with
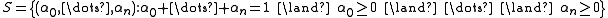 and an appropriate measure
and an appropriate measure  which assigns the simplex a volume of 1, we obtain
which assigns the simplex a volume of 1, we obtain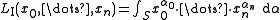
This can be simplified using divided differences of the exponential function to
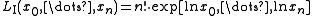 .
.Example
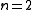
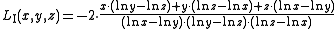 .
.Connection to other means
-
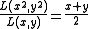 (Arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
(Arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
)
See also
- A different mean which is related to logarithms is the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
. - The logarithmic mean is a special case of the Stolarsky mean.


